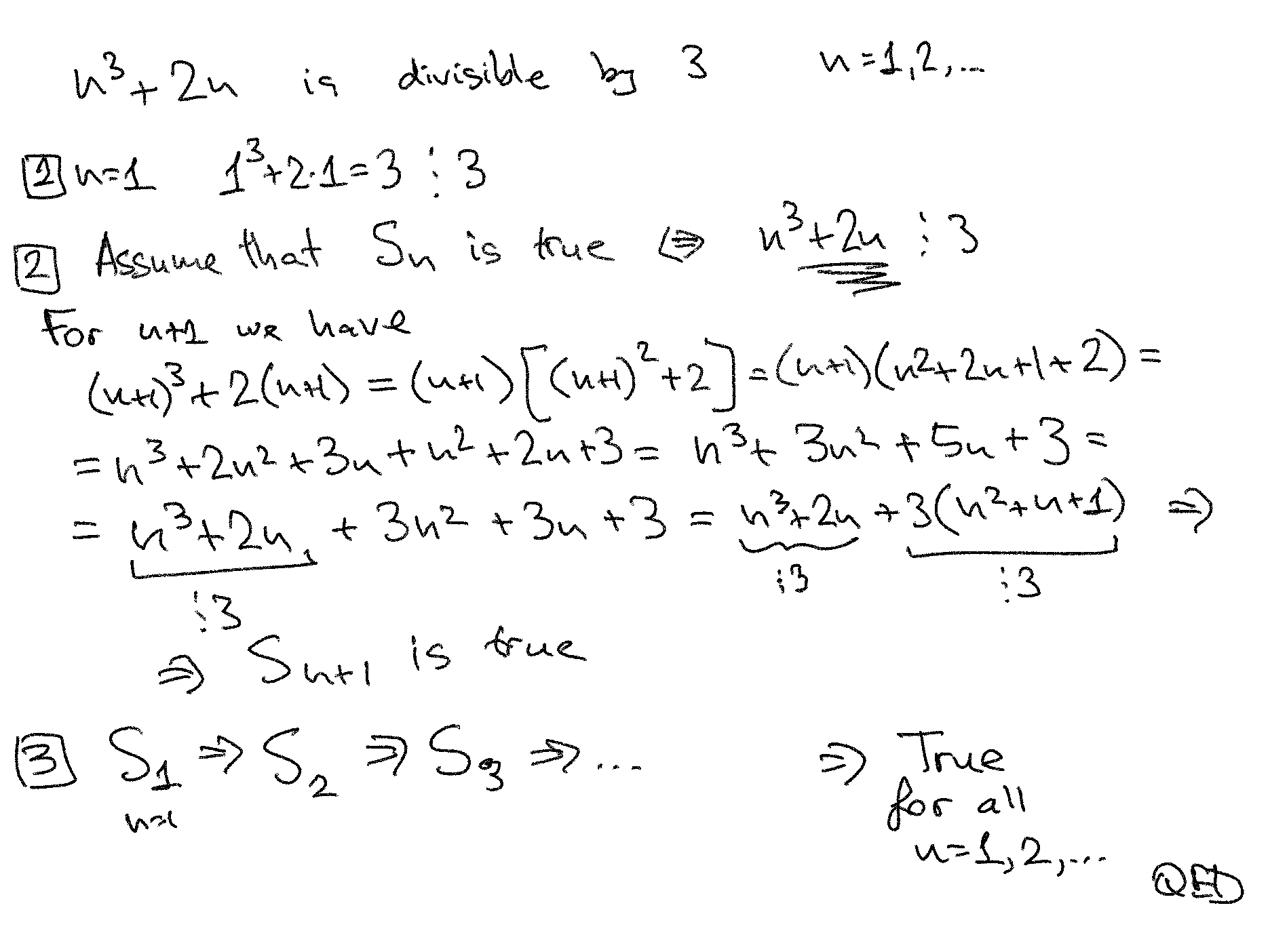📖 Elements of logic and proofs

📖 Elements of logic and proofs#

⏱ | words

References and additional materials
_images/simon1994.png

[Simon and Blume, 1994]

Appendix A1.3

_images/sundaram1996.png

[Sundaram, 1996]

Appendix A.2, A.3, A.4

The Wason selection paradox#

  • Mathematics relies on rules of logic

  • Yet, for human brain applying mathematical logic may be difficult, and dependent on the domain

_images/wason.png

  • Peter Cathcart Wason (1924 – 2003)

  • cognitive psychologist at University College, London

  • pioneered the psychology of reasoning

The Wason selection task

Given four cards showing 3, 8, blue and red faces, which cards have to be flipped over to ensure the rule if card shows even number on one side, the other side is blue is satisfied?

Let’s play Wason Selection Task at Mentimeter

Analysis of Wason selection task

  • Let \(P\) denote card shows even number on one side

  • Let \(Q\) denote the side is blue

Number

Color

\(P\)

\(Q\)

Rule is satisfied

Even

Blue

True

True

Yes

Even

Red

True

False

No

Odd

Blue

False

True

Yes

Odd

Red

False

False

Yes

  • the rule we are checking is \(P \implies Q\)

  • it is only brocken in case \(P\) is True and \(Q\) is False

  • therefore the two cards that have to be flipped are

    • Even, \(P\) is True

    • Red, \(Q\) is False

Definition

\(\implies\) denotes logical implication:
If whenever logical statment \(P\) is true, \(Q\) is also true, we write \(P \implies Q\).

Example

If \(x\) is an even number, then \(x^2\) is also an even number.

OR

\(x\) is an even \(\implies\) \(x^2\) is also even.

Necessary and Sufficient conditions#

Definition

\(P\) is a sufficient condition for \(Q\) means \(P \implies Q\)
\(P\) is a necessary condition for \(Q\) means \(Q \implies P\), or \(P \impliedby Q\)

Definition

\(P\) is said to be if and only if \(Q\) when \(P \implies Q\) and \(Q \implies P\), also written as \(P \iff Q\)

Example

\[\begin{split} x > 3 \implies x^2 >9 \text{ yet converse is not true} \\ x^2 > 9 \iff \{x > 3 \text{ or } x<-3\} \end{split}\]

Converse and contrapositive#

Definition

A logical statement \(P \implies Q\) is converse to \(Q \implies P\)

Note

There is no logical relationship between a statement and its converse!

  • bases for common logical mistakes

Example

“All cats are animals who have tails” does not imply “All animals with tails are cats”

Definition

A logical statement opposite to \(P\) is denoted \(\neg P\)

Definition

A logical statement \(\neg P \implies \neg Q\) is contrapositive to \(Q \implies P\)

Fact: Contrapositive principle

The statement \(P \implies Q\) is equivalent to the statement \((\text{not } Q) \implies (\text{not }P)\):

\[ (P \implies Q) \iff (\neg Q \implies \neg P) \]

  • this is very handy in proofs: instead of proving a statement it may be easier to prove its contrapositive

Example

\[ x > 3 \implies x^2 >9 \]

We can check that the contrapositive is also true:

\[\begin{split} \begin{array}{rcl} \neg \{x^2 >9\} & \implies & \neg\{x > 3\} \\ x^2 \leq 9 & \implies & x \leq 3 \qquad \text{! INCORRECT !} \end{array} \end{split}\]

But the contrapositive is equivalent to the original statement.

\[ \{x > 3 \implies x^2 >9\} \iff \{x^2 \leq 9 \implies \neg\{x > 3\} \} \]

Types of mathematical proofs#

Direct proof#

\(A\) is true \(\implies\) \(B\) is True \(\implies\) \(S\) is True

Example

Prove that \(p^2-1\) is divisible by 24 for all prime \(p>3\).

Proof

Note that \(p^2-1 = (p-1)(p+1)\).

  1. Since \(p\) is prime, \(p\) is odd and \(p-1\) and \(p+1\) are even. Thus, \(p^2-1\) is divisible by 2 twice.

  2. Moreover, since \(p-1\) and \(p+1\) are two consecutive even numbers, one of them is divisible not only by 2, but also 4. Thus, \(p^2-1\) is divisible by 8.

  3. Finally, since \(p-1\), \(p\), and \(p+1\) are three consecutive integers, one of them is divisible by 3.

Overall, we have that \(p^2-1 = (p-1)(p+1)\) is divisible by 2, by 4, and by 3, and thus by its product 24. \(\blacksquare\)

Note

The symbol \(\blacksquare\) marks the end of the proof, and is equivalent to the QED symbol (”quod erat demonstrandum”, or “that which was to be demonstrated”).

Proof by contradiction#

\[\begin{split} \left. \begin{array}{r} \text{Assume } S \text{ is not True }\\ A \text{ is True} \end{array} \right \} \implies \text{Contradiction} \implies \text{Assumption was wrong} \implies S \text{ is True } \end{split}\]

Example

Prove that the set of prime numbers is infinite.

Proof

The standard proof of the infinitude of the primes is attributed to Euclid and uses the fact that all integers greater than 1 have a prime factor.

Lemma: Every integer greater than 1 has a prime factor.

Proof. We argue by induction (see below) that each integer \(n > 1\) has a prime factor. For the base case \(n = 2\), 2 is prime and is a factor of itself.

Now assume \(n > 2\), all integers greater than 1 and less than \(n\) have a prime factor. To show \(n\) has a prime factor, we take cases.

Case 1: \(n\) is prime. Since \(n\) is a factor of itself, \(n\) has a prime factor when \(n\) is prime.

Case 2: \(n\) is not prime. Since \(n\) is not prime, it has a factorization \(n = ab\) where \(1 < a,b < n\). Then by the inductive hypothesis, \(a\) has a prime factor, say \(p\). Since \(a\) is divisible by \(p\) and \(n\) is divisible by \(a\), so \(n\) is divisible by \(p\). Thus \(n\) has prime factor \(p\).

Theorem: There are infinitely many primes.

Proof. (due to Euclid) To show there are infinitely many primes, we’ll show that every finite list of primes is missing a prime number, so the list of all primes can’t be finite.

Suppose \(p_1, \ldots, p_r\) is a finite list of prime numbers.

Then consider the number

\[ N = p_1 \cdot \ldots \cdot p_r + 1. \]

Since \(N > 1\), it has a prime factor \(p\) by Lemma 2.1. The prime \(p\) can’t be any of \(p_1, \ldots, p_r\) since \(N\) has remainder 1 when divided by each \(p_i\). Therefore \(p\) is a prime not on our list. We arrive at a contradiction, and thus the set of primes can’t be finite.

Proof by mathematical induction#

\[\begin{split} \left. \begin{array}{r} S_1 \text{ is True }\\ S_n \text{ is True} \implies S_{n+1} \text{ is True} \end{array} \right \} \implies S_k \text{ is True for all } k=1,2,3,\dots \end{split}\]

Example

Prove that \(n^3+2n\) is divisible by 3 for all \(n=1,2,\dots\)

Proof

  1. Base of the induction: For \(n=1\), we have \(1^3+2\cdot 1 = 3\) which is divisible by 3. \(S_1\) is true.

  2. Induction step. Assume that \(n^3+2n\) is divisible by 3 for some \(n\), in other words that \(S_n\) is true. The job is to show that it is also true for \(n+1\), i.e. that \(S_{n+1}\) is true.

Writing the initial expression \(n^3+2n\) for \(n+1\) we have

\[ (n+1)^3+2(n+1) = (n+1)(n^2+2n+1)+2n+2 = \]
\[ =n^3+3n^2+3n+1 +2n+2 = (n^3+2n) + 3(n^2+n+1) \]

The second term is obviously divisible by 3, and the first term is divisible by 3 by the induction hypothesis. Thus, we have shown that \(S_{n+1}\) is also true.

  1. By the principle of mathematical induction, we have thus shown that \(n^3+2n\) is divisible by 3 for all \(n=1,2,\dots\) \(\blacksquare\)

Note

Be careful to make sure that the induction step holds for all \(n\) starting with the base case \(n=1\).

Example

Statement: all horses are the same color.

  1. Base of the induction: for \(n=1\) there is only one horse, and only one color, so the statement holds for \(n=1\).

  2. Induction step. Assume that any group of \(n\) horses are the same color. We can show that the same is true for any group of \(n+1\) horses.

Indeed, in the group of \(n+1\) hourses, take all but the one hourse: by induction hypothesis this subgroup of \(n\) horses is the same color. Now take all but another horse: by induction hypothesis this second subgroup of \(n\) horses is the same color. Thus, no different color can be observed, and therefore the groupd of \(n+1\) horse is the same color.

  1. By the principle of mathematical induction, we have thus shown that all horses are the same color.

What is wrong with the proof?

The induction step fails for \(n=2\) when each of the two subgroups has only one horse, and thus the subgroups may in fact have two different colors.

Hand written notes from the lecture

_images/w1_1.png _images/w1_2.png