📖 Constrained optimization

📖 Constrained optimization#

⏱ | words

References and additional materials
_images/simon1994.png

[Simon and Blume, 1994]

Chapters 16.2, whole of chapter 18, 19.3

_images/sundaram1996.png

[Sundaram, 1996]

Chapter 5 and 6

Setting up a constrained optimization problem#

Let’s start with recalling the definition of a general optimization problem

Definition

The general form of the optimization problem is

\[\begin{split} V(\theta) = \max_{x} f(x,\theta) \\ \text {subject to} \\ g_i(x,\theta) = 0, \; i\in\{1,\dots,I\}\\ h_j(x,\theta) \le 0, \; j\in\{1,\dots,J\} \end{split}\]

where:

  • \(f(x,\theta) \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\) is an objective function

  • \(x \in \mathbb{R}^N\) are decision/choice variables

  • \(\theta \in \mathbb{R}^K\) are parameters

  • \(g_i(x,\theta) = 0, \; i\in\{1,\dots,I\}\) where \(g_i \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\), are equality constraints

  • \(h_j(x,\theta) \le 0, \; j\in\{1,\dots,J\}\) where \(h_j \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\), are inequality constraints

  • \(V(\theta) \colon \mathbb{R}^K \to \mathbb{R}\) is a value function

Today we focus on the problem with constrants, i.e. \(I+J>0\)

The obvious classification that we follow

  • equality constrained problems, i.e. \(I>0\), \(J=0\)

  • inequality constrained problems, i.e. \(J>0\), which can include equalities as special case

Note

Note that every optimization problem can be seen as constrained if we define the objective function to have the domain that coincides with the admissible set.

\[\begin{split} \begin{array}{c} \max_x f(x): \mathbb{R}^N \to \mathbb{R} \\ \text {subject to} \\ g_i(x) = 0, \; i\in\{1,\dots,I\}\\ h_j(x) \le 0, \; j\in\{1,\dots,J\} \end{array} \end{split}\]

is equivalent to

\[\begin{split} \begin{array}{c} \max_x f(x): A \to \mathbb{R} \\ A = \big\{x \in \mathbb{R}^N \colon g_i(x) = 0, \; i\in\{1,\dots,I\} \text{ and } h_j(x) \le 0, \; j\in\{1,\dots,J\}\big\} \end{array} \end{split}\]

Constrained Optimization = economics#

A major focus of econ: the optimal allocation of scarce resources

  • optimal = optimization

  • scarce = constrained

Standard constrained problems:

  • Maximize utility given budget

  • Maximize portfolio return given risk constraints

  • Minimize cost given output requirement

Example

Maximization of utility subject to budget constraint

\[ % \max u(x_1, x_2) \; \text{ such that } \; p_1 x_1 + p_2 x_2 \leq m % \]

  • \(p_i\) is the price of good \(i\), assumed \(> 0\)

  • \(m\) is the budget, assumed \(> 0\)

  • \(x_i \geq 0\) for \(i = 1,2\)

  • let \(u(x_1, x_2) = \alpha \log(x_1) + \beta \log(x_2)\), \(\alpha>0\), \(\beta>0\)

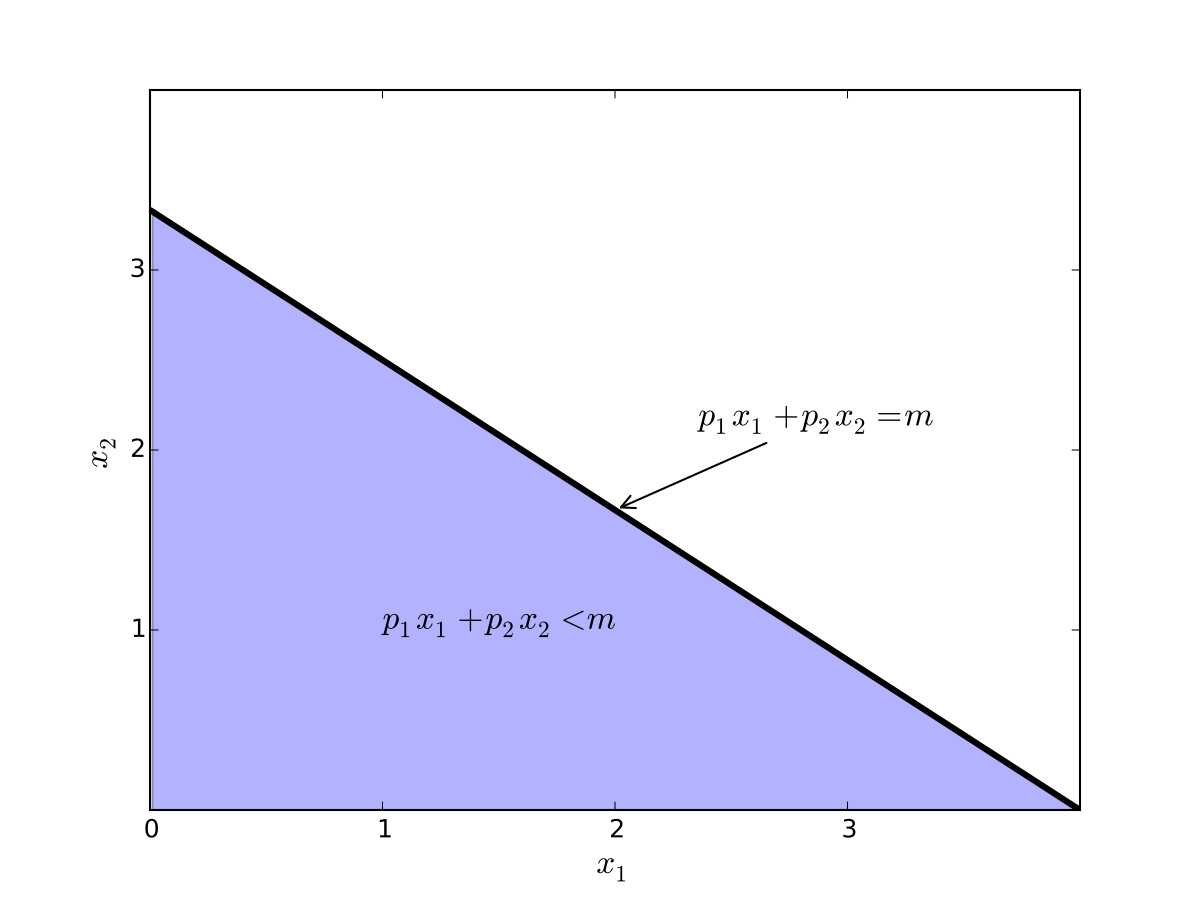
_images/budget_set_1.png

Fig. 63 Budget set when, \(p_1=0.8\), \(p_2 = 1.2\), \(m=4\)#

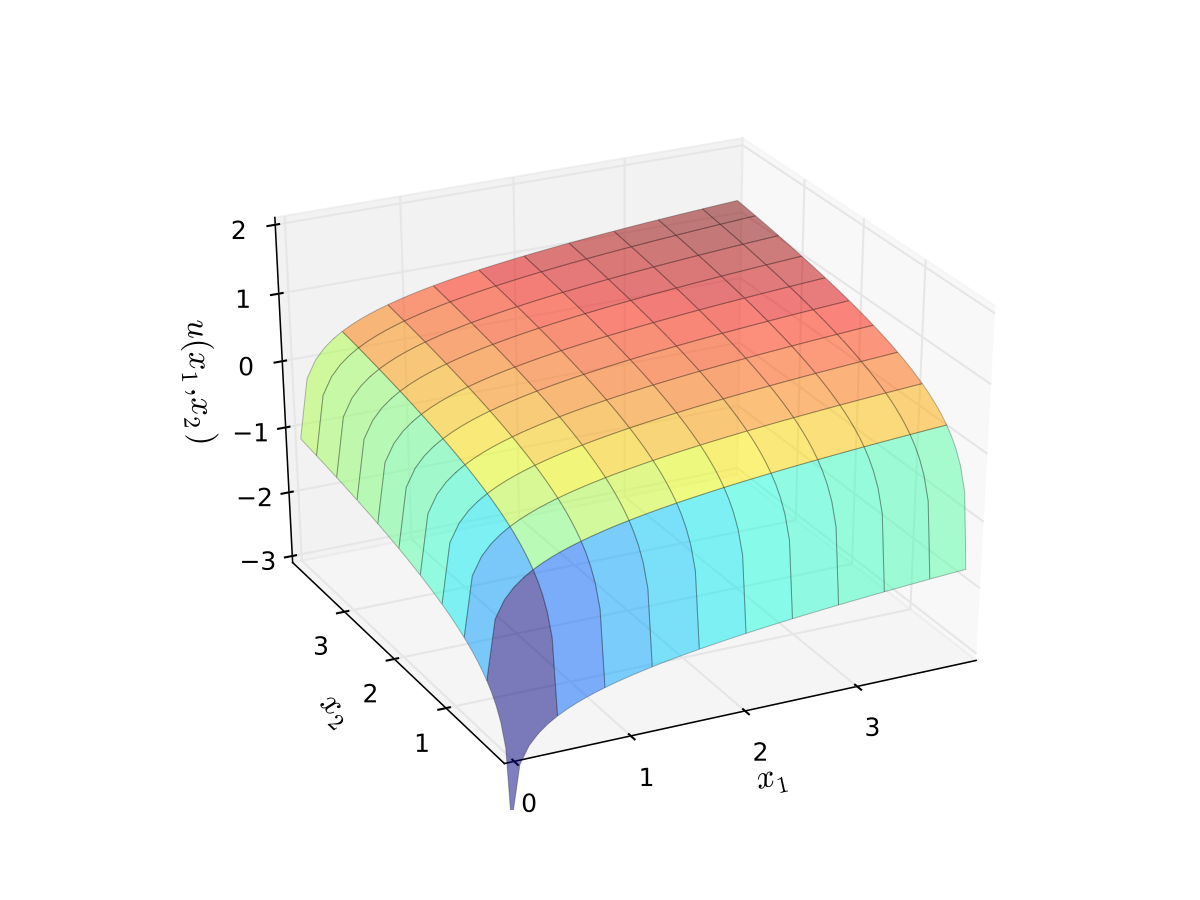
_images/log_util.png

Fig. 64 Log utility with \(\alpha=0.4\), \(\beta=0.5\)#

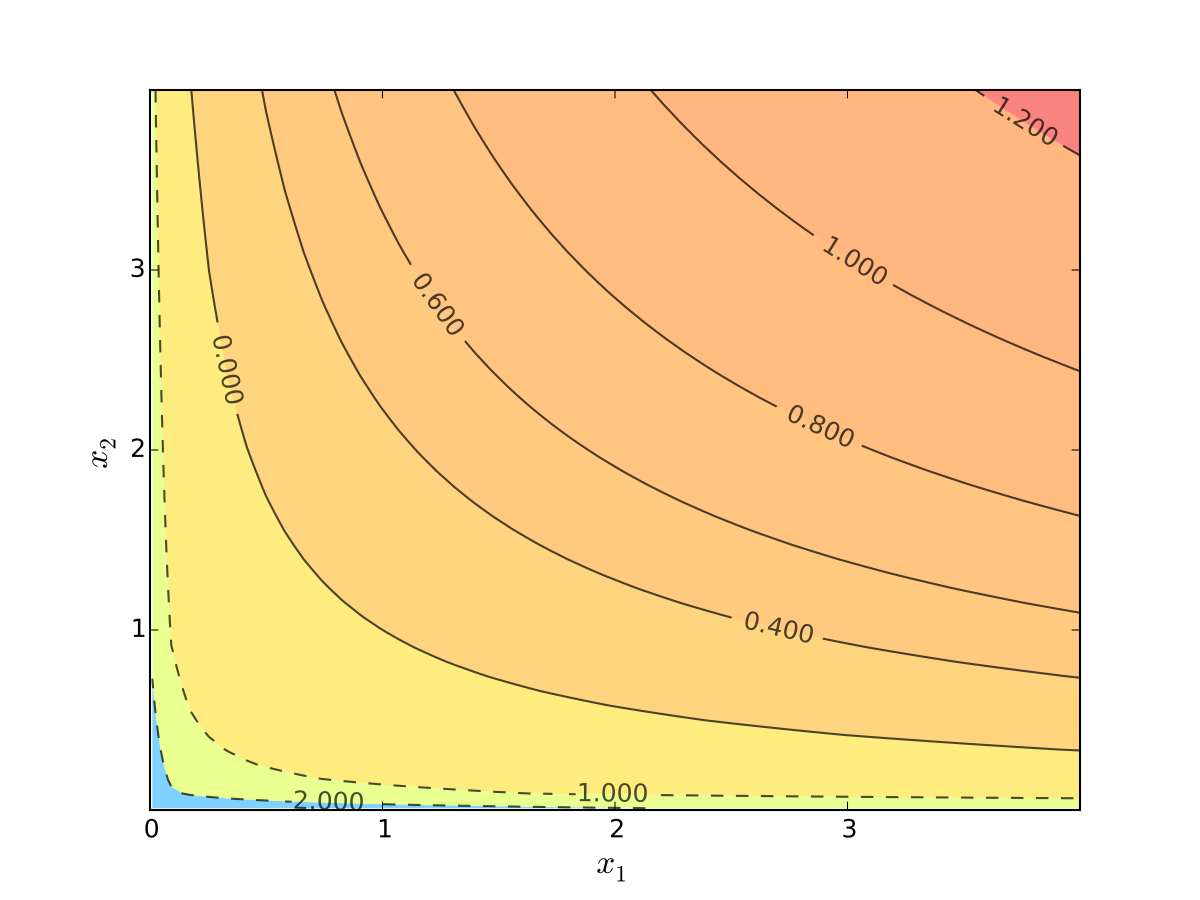
_images/log_util_contour.png

Fig. 65 Log utility with \(\alpha=0.4\), \(\beta=0.5\)#

We seek a bundle \((x_1^\star, x_2^\star)\) that maximizes \(u\) over the budget set

That is,

\[ % \alpha \log(x_1^\star) + \beta \log(x_2^\star) \geq \alpha \log(x_1) + \beta \log(x_2) % \]

for all \((x_1, x_2)\) satisfying \(x_i \geq 0\) for each \(i\) and

\[ % p_1 x_1 + p_2 x_2 \leq m % \]

Visually, here is the budget set and objective function:

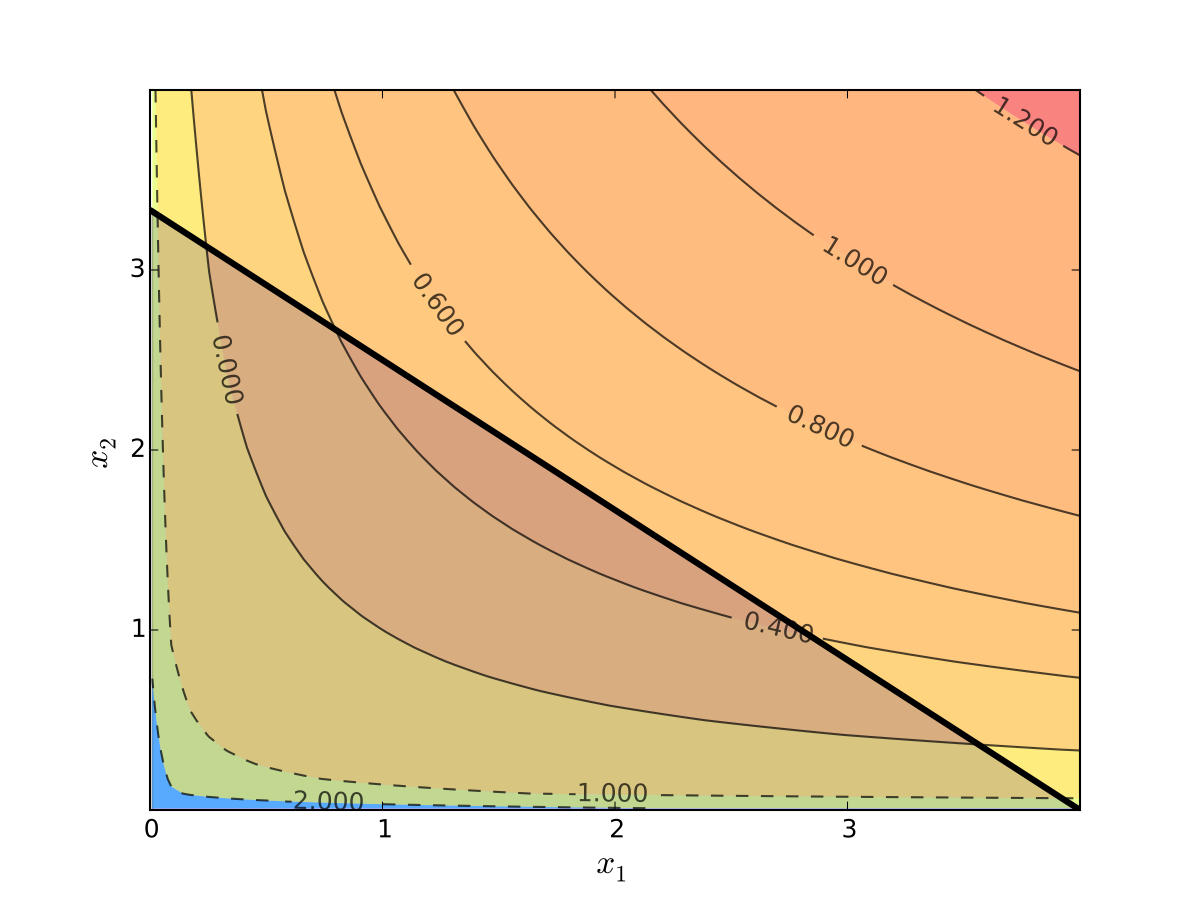
_images/budget_set_3.png

Fig. 66 Utility max for \(p_1=1\), \(p_2 = 1.2\), \(m=4\), \(\alpha=0.4\), \(\beta=0.5\)#

First observation: \(u(0, x_2) = u(x_1, 0) = u(0, 0) = -\infty\)

  • Hence we need consider only strictly positive bundles

Second observation: \(u(x_1, x_2)\) is strictly increasing in both \(x_i\)

  • Never choose a point \((x_1, x_2)\) with \(p_1 x_1 + p_2 x_2 < m\)

  • Otherwise can increase \(u(x_1, x_2)\) by small change

Hence we can replace \(\leq\) with \(=\) in the constraint

\[ % p_1 x_1 + p_2 x_2 \leq m \quad \text{becomes} \quad p_1 x_1 + p_2 x_2 = m % \]

Implication: Just search along the budget line

Substitution Method#

Substitute constraint into objective function and treat the problem as unconstrained

This changes

\[ % \max_{x_1, x_2} \left\{ \alpha \log(x_1) + \beta \log(x_2) \right\} \text{ such that } \; p_1 x_1 + p_2 x_2 = m % \]

into

\[ % \max_{x_1} \left\{ \alpha \log(x_1) + \beta \log((m - p_1x_1) / p_2) \right\} % \]

Since all candidates satisfy \(x_1 > 0\) and \(x_2 > 0\), the domain is

\[ 0 < x_1 < \frac{m}{p_1} \]
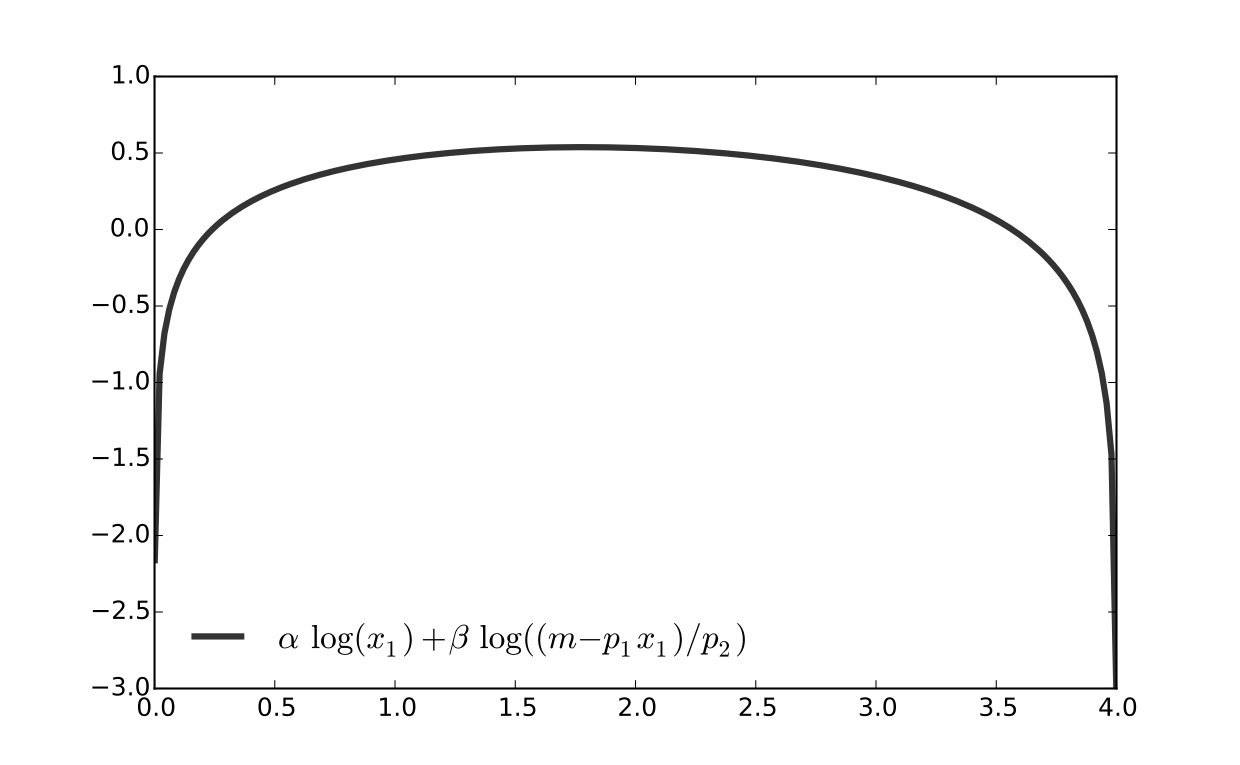
_images/one_dim_budget.png

Fig. 67 Utility max for \(p_1=1\), \(p_2 = 1.2\), \(m=4\), \(\alpha=0.4\), \(\beta=0.5\)#

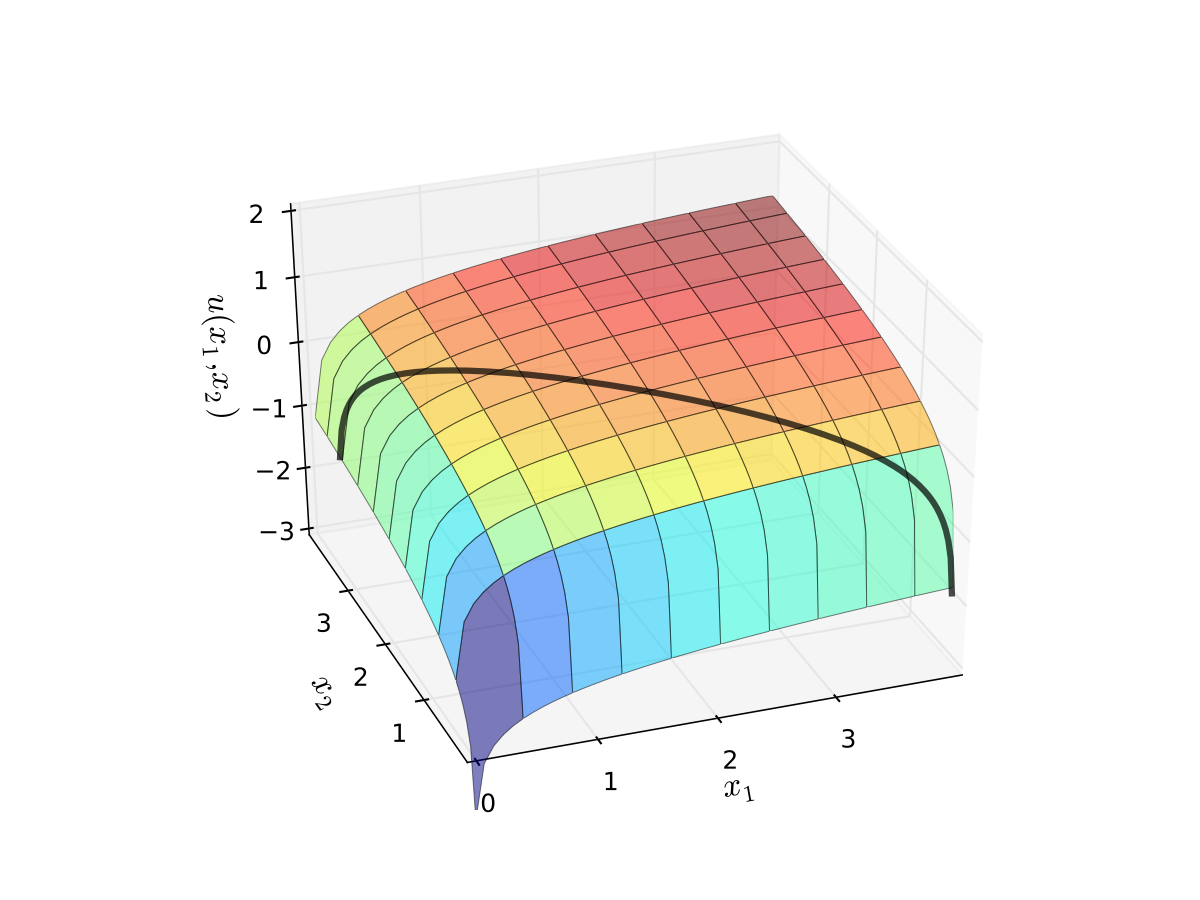
_images/log_util_budget_line.png

Fig. 68 Utility max for \(p_1=1\), \(p_2 = 1.2\), \(m=4\), \(\alpha=0.4\), \(\beta=0.5\)#

First order condition for

\[ % \max_{x_1} \left\{ \alpha \log(x_1) + \beta \log((m - p_1x_1) / p_2) \right\} % \]

gives

\[ % x_1^\star = \frac{\alpha}{\alpha + \beta} \cdot \frac{m}{p_1} % \]

Exercise: Verify

Exercise: Check second order condition (strict concavity)

Substituting into \(p_1 x_1^\star + p_2 x_2^\star = m\) gives

\[ % x_2^\star = \frac{\beta}{\beta + \alpha} \cdot \frac{m}{p_2} % \]
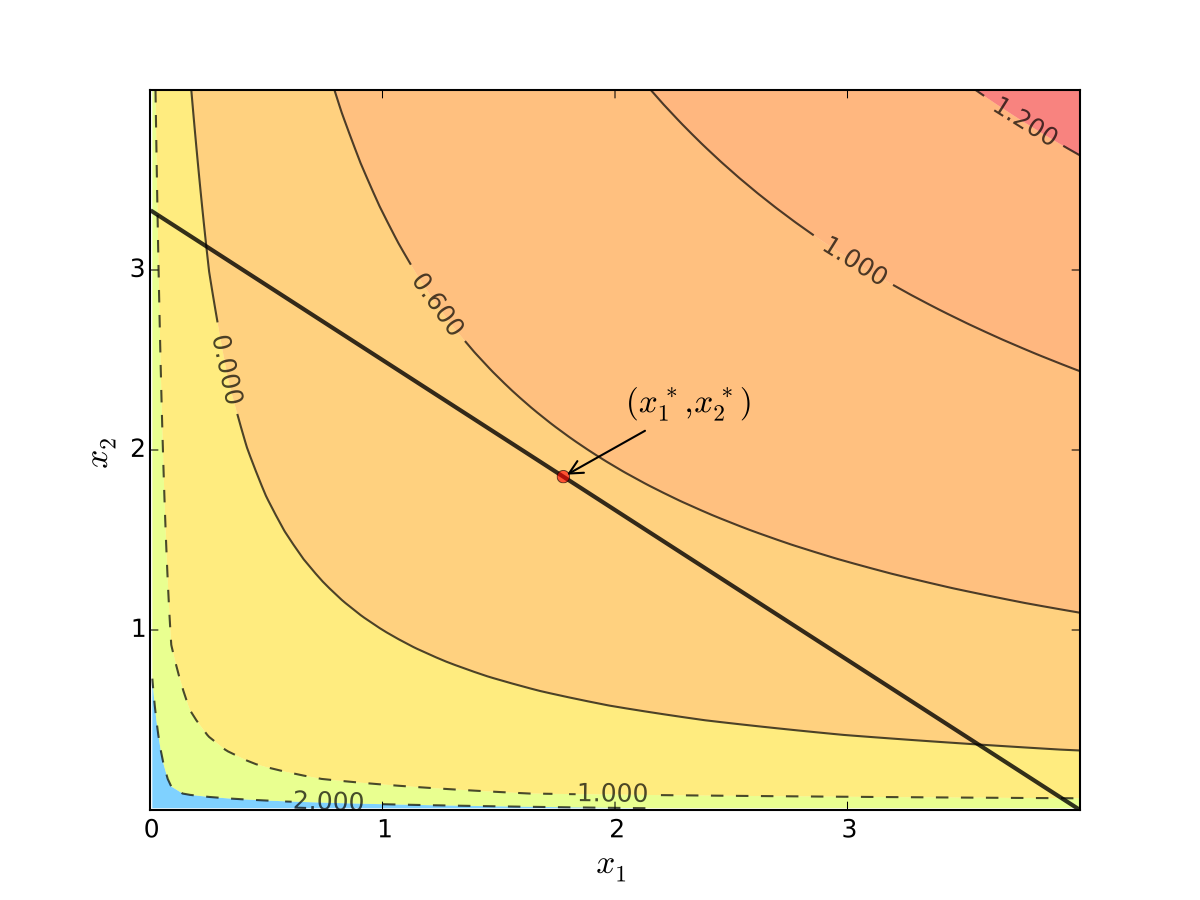
_images/log_util_optimizer.png

Fig. 69 Maximizer for \(p_1=1\), \(p_2 = 1.2\), \(m=4\), \(\alpha=0.4\), \(\beta=0.5\)#

Substitution method: algorithm#

How to solve

\[\begin{split} % \max_{x_1, x_2} \; f(x_1, x_2) \\ \text{ such that } g(x_1, x_2) = 0 % \end{split}\]

Steps:

  1. Write constraint as \(x_2 = h(x_1)\) for some function \(h\)

  • Solve univariate problem \(\max_{x_1} f(x_1, h(x_1))\) to get \(x_1^\star\)

  1. Plug \(x_1^\star\) into \(x_2 = h(x_1)\) to get \(x_2^\star\)

Limitations: substitution doesn’t always work

Example

Suppose that \(g(x_1, x_2) = x_1^2 + x_2^2 - 1\)

Step 1 from the cookbook says

use \(g(x_1, x_2) = 0\) to write \(x_2\) as a function of \(x_1\)

But \(x_2\) has two possible values for each \(x_1 \in (-1, 1)\)

\[ % x_2 = \pm \sqrt{1 - x_1^2} % \]

In other words, \(x_2\) is not a well defined function of \(x_1\)

As we meet more complicated constraints such problems intensify

  • Constraint defines complex curve in \((x_1, x_2)\) space

  • Inequality constraints, etc.

We need more general, systematic approach

Tangency and relative slope conditions#

Optimization approach based on tangency of contours and constraints

Example

Consider again the problem

\[\begin{split} \max_{x_1, x_2} \left\{ \alpha \log(x_1) + \beta \log(x_2) \right\} \\ \text{ such that } p_1 x_1 + p_2 x_2 = m \end{split}\]

Turns out that the maximizer has the following property:

  • budget line is tangent to an indifference curve at maximizer

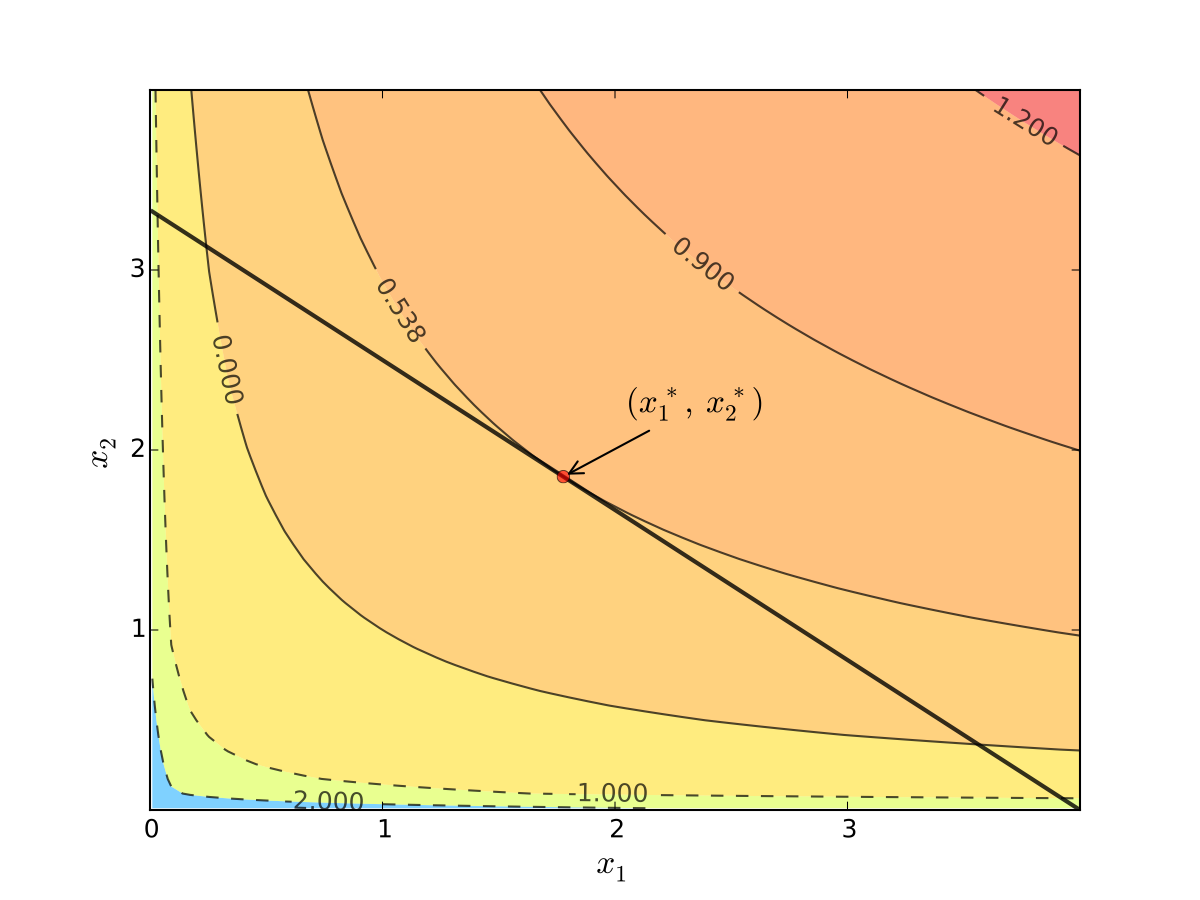
_images/log_util_maximizer_tangent.png

Fig. 70 Maximizer for \(p_1=1\), \(p_2 = 1.2\), \(m=4\), \(\alpha=0.4\), \(\beta=0.5\)#

In fact this is an instance of a general pattern

Notation: Let’s call \((x_1, x_2)\) interior to the budget line if \(x_i > 0\) for \(i=1,2\) (not a “corner” solution, see below)

In general, any interior maximizer \((x_1^\star, x_2^\star)\) of differentiable utility function \(u\) has the property: budget line is tangent to a contour line at \((x_1^\star, x_2^\star)\)

Otherwise we can do better:

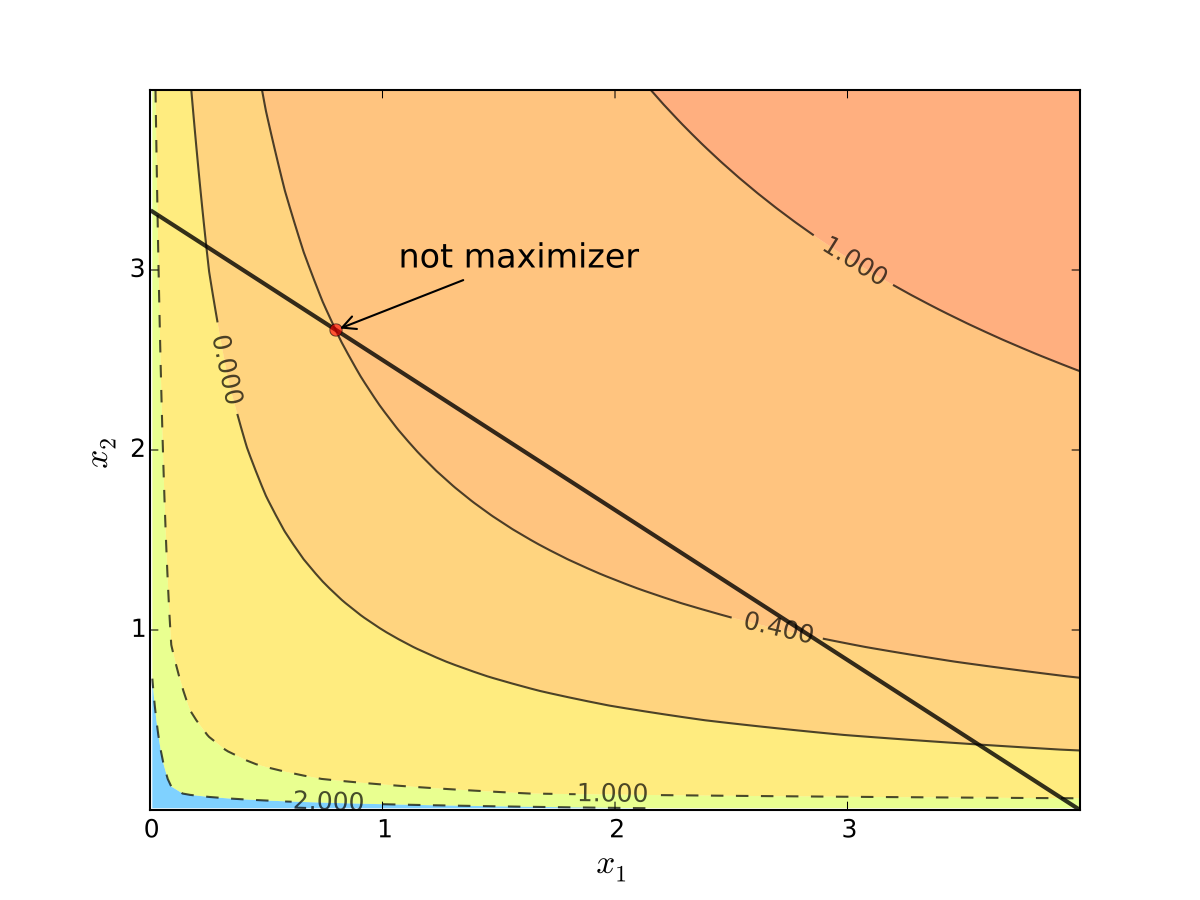
_images/log_util_not_maximizer.png

Fig. 71 When tangency fails we can do better#

Necessity of tangency often rules out a lot of points

We exploit this fact to build intuition and develop more general method

Relative Slope Conditions#

Consider an equality constrained optimization problem where objective and constraint functions are differentiable:

\[\begin{split} % f(x_1, x_2) \longrightarrow \max_{x_1, x_2} \\ \text{ such that } g(x_1, x_2) = 0 % \end{split}\]

How to develop necessary conditions for optima via tangency?

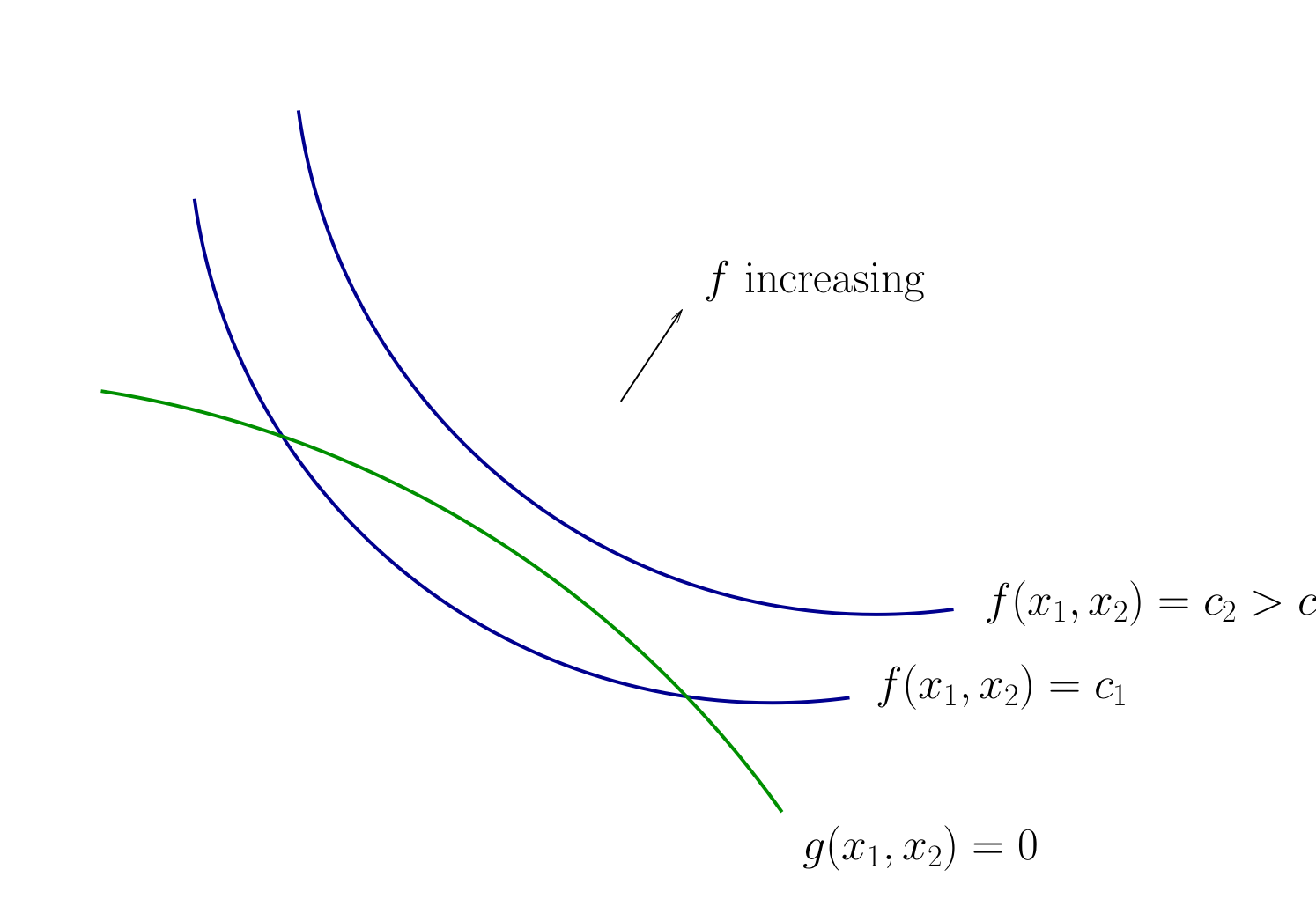
_images/tangency_1.png

Fig. 72 Contours for \(f\) and \(g\)#

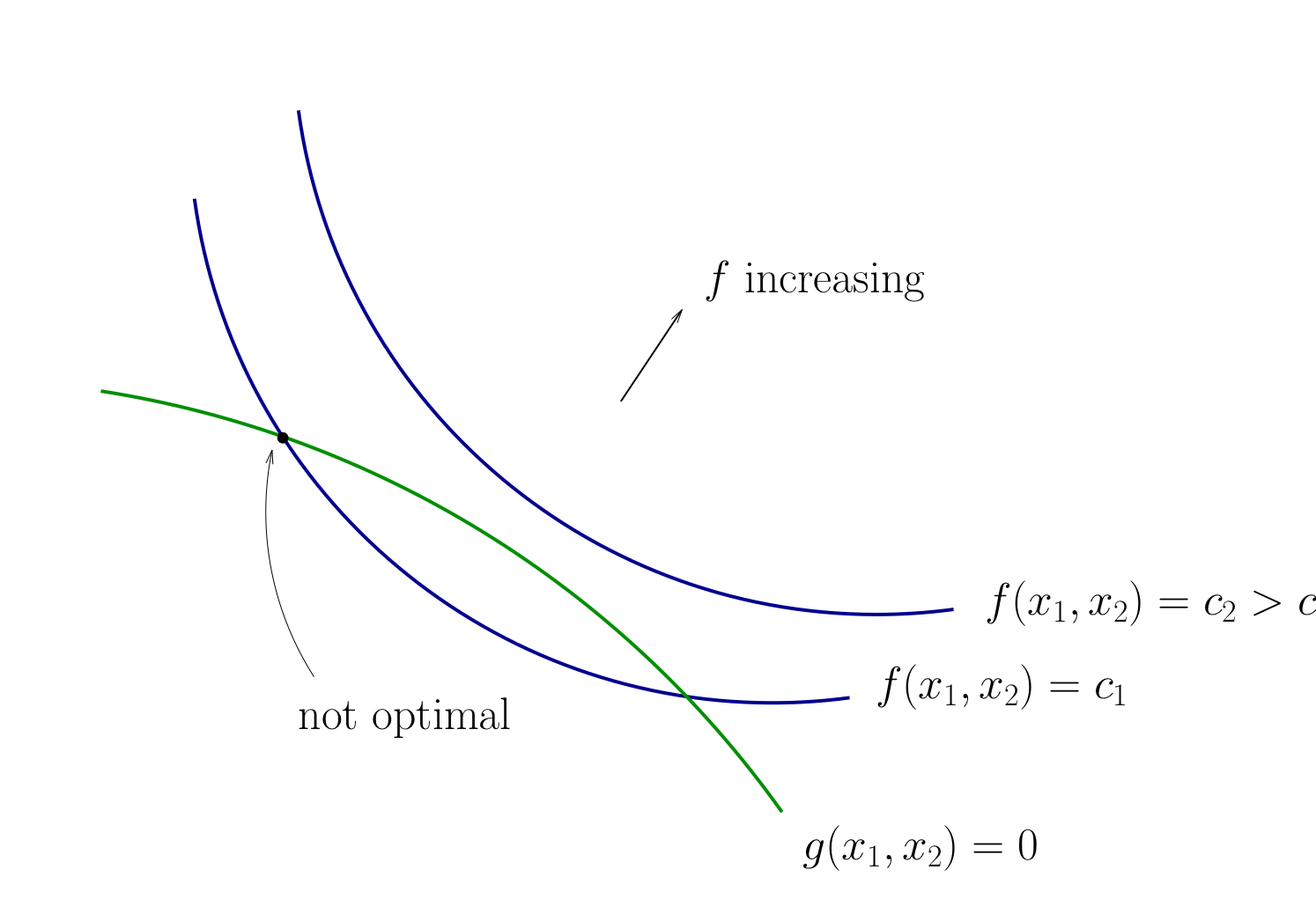
_images/tangency_2.png

Fig. 73 Contours for \(f\) and \(g\)#

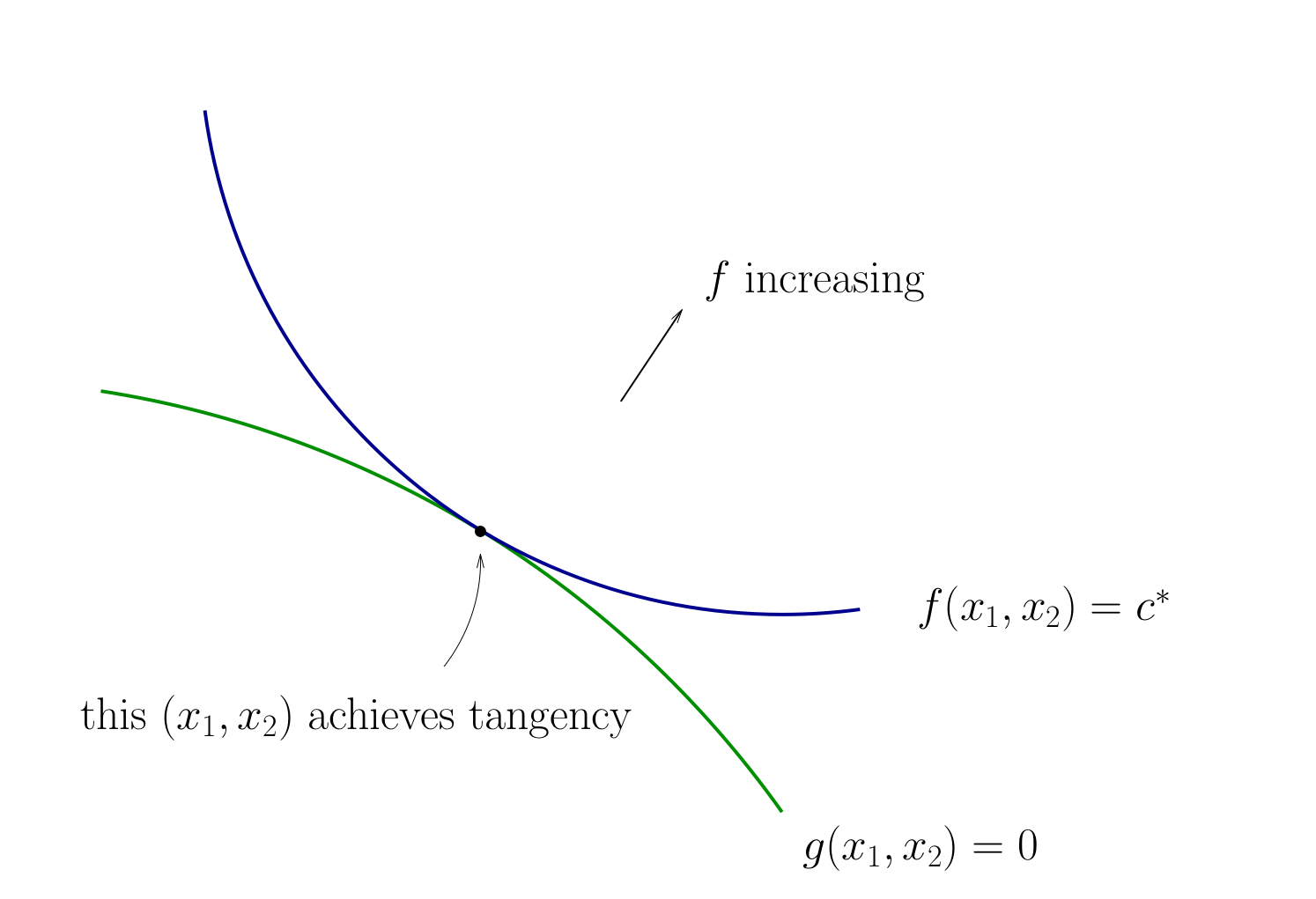
_images/tangency_3.png

Fig. 74 Tangency necessary for optimality#

How do we locate an optimal \((x_1, x_2)\) pair?

Diversion: derivative of an implicit function

To continue with the tangency approach we need to know how to differentiate an implicit function \(x_2(x_1)\) which is given by a contour line of the utility function \(f(x_1, x_2)=c\)

Let’s approach this task in the following way

  • utility function is given by \(f \colon \mathbb{R}^2 \to \mathbb{R}\)

  • the contour line is given by \(f(x_1,x_2) = c\) which defines an implicit function \(x_1(x_2)\)

  • let map \(g \colon \mathbb{R} \to \mathbb{R}^2\) given by \(g(x_2) = \big[x_1(x_2),x_2\big]\)

The total derivative matrix of \(f \circ g\) can be derived using the chain rule

\[\begin{split} Dg(x_2) = \left( \begin{array}{c} \frac{d x_1}{d x_2} \\ 1 \end{array} \right) \\ Df(x) = \left( \frac{\partial f}{\partial x_1}(x), \frac{\partial f}{\partial x_2}(x) \right) = \big(f_1(x),f_2(x)\big) \\ D(f \circ g)(x) = Df(x) \cdot Dg(x) = f_1\big(g(x_2)\big) \frac{d x_1}{d x_2} + f_2\big(g(x_2)\big) \end{split}\]

Differentiating the equation \(f(x_1,x_2) = c\) on both sides with respect to \(x_2\) gives \(D(f \circ g)(x) = 0\), thus leading to the final expression for the derivative of the implicit function

\[ \frac{d x_1}{d x_2}(x_2) = - \frac{f_2(x_1,x_2)}{f_1(x_1,x_2)} = - \frac{f_2(x_1,x_2)}{f_1(x_1,x_2)} \]
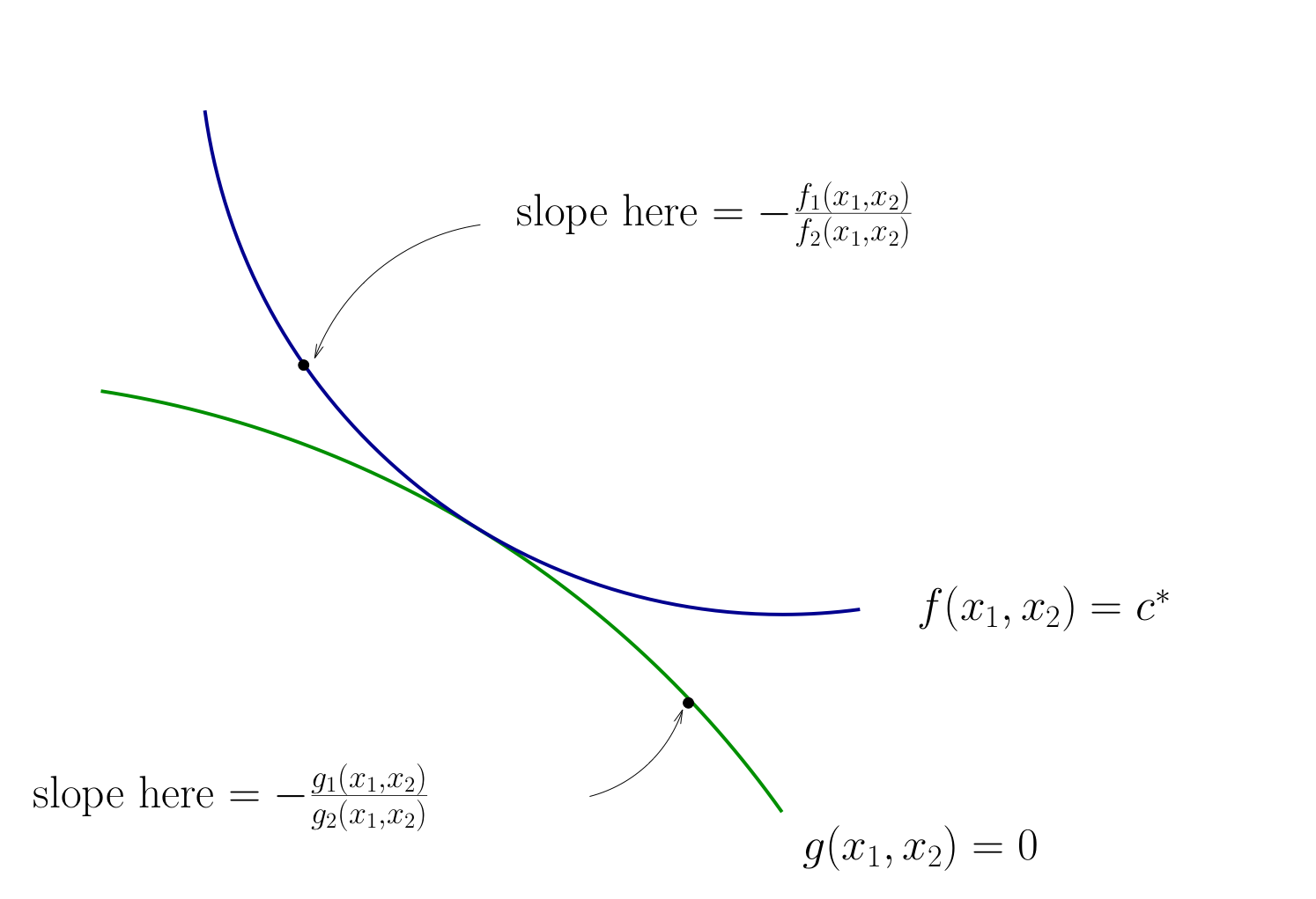
_images/tangency_4.png

Fig. 75 Slope of contour lines#

Let’s choose \((x_1, x_2)\) to equalize the slopes

That is, choose \((x_1, x_2)\) to solve

\[ % - \frac{f_1(x_1, x_2)} {f_2(x_1, x_2)} = - \frac{g_1(x_1, x_2)} {g_2(x_1, x_2)} % \]

Equivalent:

\[ % \frac{f_1(x_1, x_2)} {f_2(x_1, x_2)} = \frac{g_1(x_1, x_2)} {g_2(x_1, x_2)} % \]

Also need to respect \(g(x_1, x_2) = 0\)

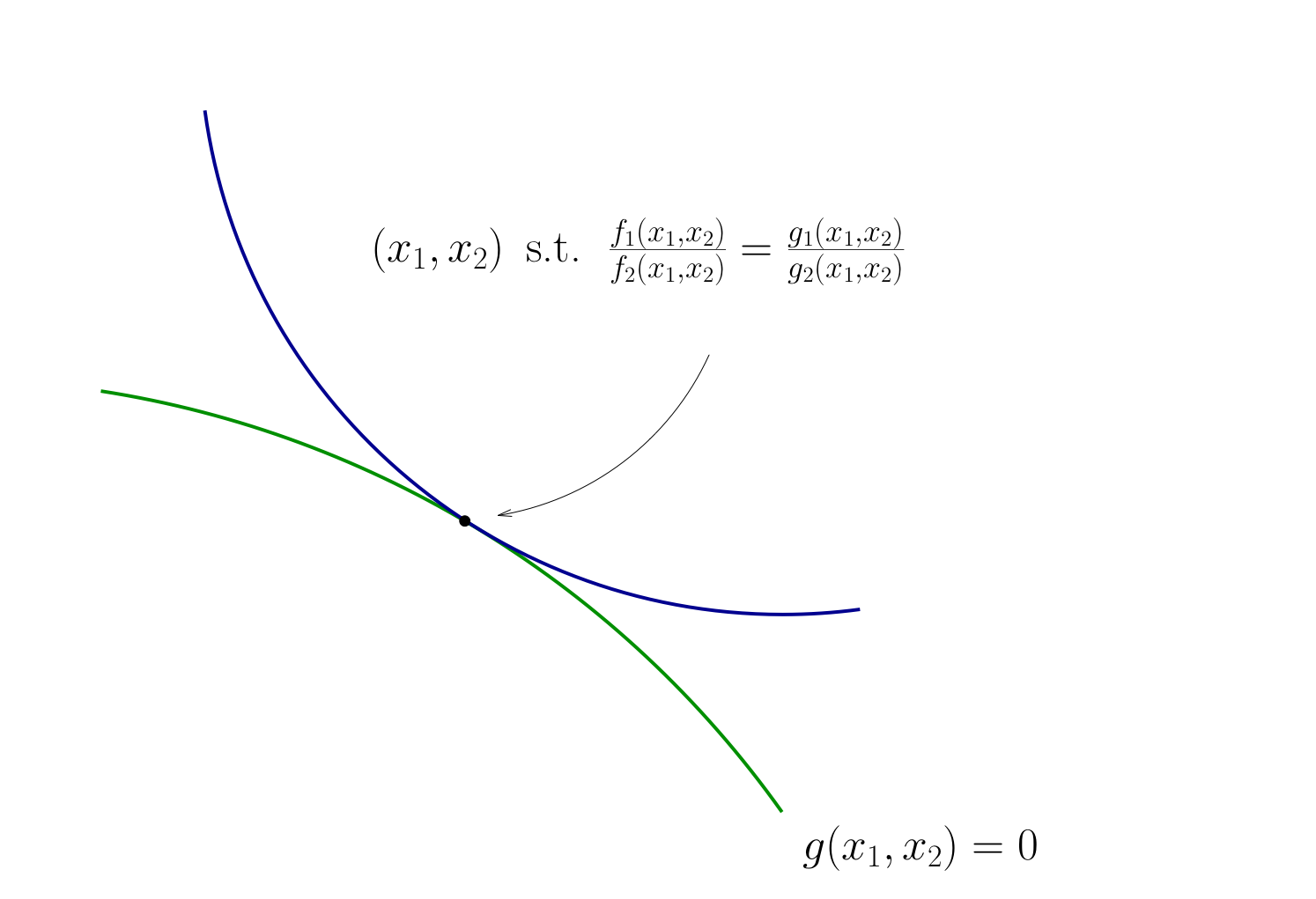
_images/tangency_5.png

Fig. 76 Condition for tangency#

Tangency condition algorithm#

In summary, when \(f\) and \(g\) are both differentiable functions, to find candidates for optima in

\[ % \max_{x_1, x_2} f(x_1, x_2) % \]
\[ % \text{ such that } \; g(x_1, x_2) = 0 % \]

  1. (Impose slope tangency) Set

\[ % \frac{f_1(x_1, x_2)}{f_2(x_1, x_2)} = \frac{g_1(x_1, x_2)}{g_2(x_1, x_2)} % \]

  1. (Impose constraint) Set \(g(x_1, x_2) = 0\)

  2. Solve simultaneously for \((x_1, x_2)\) pairs satisfying these conditions

Example

Consider again

\[ % \max_{x_1, x_2} \left\{ \alpha \log(x_1) + \beta \log(x_2) \right\} % \]
\[ % \text{ such that } \; p_1 x_1 + p_2 x_2 - m = 0 % \]

Then

\[ % \frac{f_1(x_1, x_2)}{f_2(x_1, x_2)} = \frac{g_1(x_1, x_2)}{g_2(x_1, x_2)} \quad \iff \quad \frac{\alpha}{\beta} \frac{x_2}{x_1} = \frac{p_1}{p_2} % \]

Solving simultaneously with \(p_1 x_1 + p_2 x_2 = m\) gives

\[ % x_1^\star = \frac{\alpha}{\alpha + \beta} \cdot \frac{m}{p_1} \quad \text{and} \quad x_2^\star = \frac{\beta}{\beta + \alpha} \cdot \frac{m}{p_2} % \]

Same as before…

This approach can be applied to maximization as well as minimization problems

Note

The methods described here

  • substitution method

  • tangency/relative slope method

are applicable to simple constrained optimization problems with intuitive constraints

But what about more complicated problems? Necessary and sufficient first order conditions? Second order conditions?

We need more general approach for that \(\longrightarrow\) the method of Lagrange multipliers

Contents