🔬 Tutorial problems alpha \alpha

🔬 Tutorial problems alpha \(\alpha\)#

Note

This problems are designed to help you practice the concepts covered in the lectures. Not all problems may be covered in the tutorial, those left out are for additional practice on your own.

\(\alpha\).1#

This is an exercise on necessary and sufficient conditions. Start with some definitions from geormetry:

  • a quadrilateral is a planar figure made up of four line segments connected to form a closed shape. Consider only simple quadrilaterals without self-intersections.

  • a quadrilateral with a pair of parallel sides is called a trapezoid

  • a quadrilateral with two pais of parallel sides is called a parallelogram

  • a parallelogram with right angles is called a rectangle

  • a rectangle with all sides of the same length is called a square

  • a parallelogram with all sides of the same length is called a rhombus

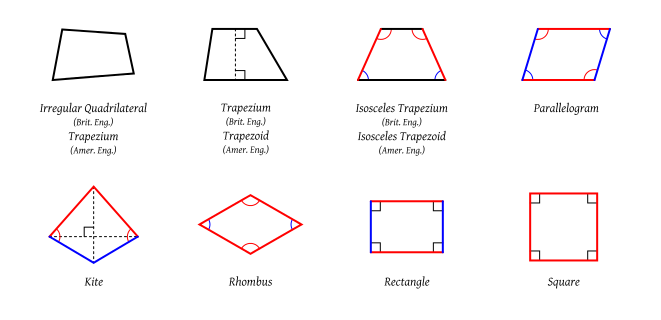
illustration

For each of the statements below determine if they are True or False. For those which are False, provide a counterexample.

  1. Sufficient condition for a quadrilateral to be a square is for it to be a rhombus.

  2. Necessary condition for a quadrilateral to be a square is for it to be a rectangle.

  3. Sufficient condition for a quadrilateral to be a rectangle is for it to be a parallelogram.

  4. Necessary condition for a quadrilateral to be a rectangle is for it to be a parallelogram.

  5. Necessary condition for a quadrilateral to be a parallelogram is for it to be a trapezoid.

  6. Sufficient condition for a quadrilateral to be a parallelogram is for it to be a square.

  7. Necessary condition for a quadrilateral to be a trapezoid is for it to be a rhombus.

  8. Necessary condition for a quadrilateral to be a rectangle is for it to be a trapezoid.

  9. Necessary and sufficient conditions for a quadrilateral to be a square are for it to simultaneously be a rectangle and a rhombus.

Review the definitions from the lecture on logic and proofs.

Use the following notation:

  • \(T\) trapezoid

  • \(P\) parallelogram

  • \(R\) rectangle

  • \(S\) square

  • \(B\) rhombus

Inspecting the conditions in the definitions we have the following implications:

\[ T \impliedby P \impliedby R \impliedby S \implies B \implies P \]

It is important to stare at these implications and convince your that you agree with each \(\implies\) and each \(\impliedby\).

Therefore correct answers are

  1. False. We don’t have \(B \implies S\); counterexample is a rhombus without right angles

  2. True. We do have \(R \impliedby S\)

  3. False. We don’t have \(P \implies R\); counterexample is a parallelogram without right angles

  4. True. We do have \(P \impliedby R\)

  5. True. We do nave \(T \impliedby P\)

  6. True. We do have \(S \implies P\) (through intermediate \(R\))

  7. False. We do have \(B \impliedby T\); counterexample is a trapezoid with bases of different lengths

  8. True. We do have \(T \impliedby R\) (through intermediate \(P\))

  9. True. We do have \((R \text{ and } B) \impliedby S\) and \((R \text{ and } B) \implies S\)

\(\alpha\).2#

Using direct proof, show that the difference between a cube of a natural number greater than one, \(n=2,3,\dots\), and the number itself is divisible by 6.

Factor the expression \(n^3-n\) and use the property of the consecutive natural numbers.

Denote the given number \(p\). Simple algebra gives \(p = n^3-n = n(n^2-1) = (n-1)n(n+1)\). For \(n = 2,3,\dots\), we conclude that \(p\) is a product of three consecutive natural numbers.

It is easy to show that among \(k\) consecutive natural numbers at least one is divisible by \(k\) (this can be proven by contradiction using the pigeonhole principle and the number of non-zero remainders).

From the above, it follows that at least one number among \(n-1\), \(n\), and \(n+1\) is divisible by 3, and by considering any subsequence of two elements, at least one number is divisible by 2. Therefore, their product \(p\) is divisible by both 2 and 3, that is by 6. \(\blacksquare\)

\(\alpha\).3#

Prove by contradiction that \(\sqrt{3}\) is an irrational number (so that is it can not be represented by a ratio of two whole numbers).

Assume the opposite, namely that \(\sqrt{3} = \frac{p}{q}\) where without loss of generality whole numbers \(p\) and \(q\) do not have common factors.

  1. Assume that \(\sqrt{3} = \frac{p}{q}\) where \(p\) ad \(q\) are whole numbers.

  2. Without loss of generality we can choose \(p\) and \(q\) such that they do not have common factors, otherwise these factors can be cancelled out.

  3. Then \(\frac{p^2}{q^2} = 3\), and so \(3q^2 = p^2 \iff p^2\) is a multiple of 3.

  4. All components in prime decomposition of \(p^2\) enter in pairs because it is a square, therefore there must be an even number of 3’s in the factorization of \(p^2\) \(\implies\) \(p\) is a multiple of 3 itself.

  5. Therefore we can find a whole number \(r\) such that \(p = 3r\), and substitute to get \(3q^2 = 9r^2 \implies q^2 = 3r^2\).

  6. Now the same arguments applied to \(q\) let us conclude that \(q\) is also a multiple of 3.

  7. This contradicts our choice of \(p\) and \(q\) not having common factors!

  8. Therefore our assumption that \(\sqrt{3} = \frac{p}{q}\) is false, and thus \(\sqrt{3}\) is indeed an irrational number. \(\blacksquare\)

\(\alpha\).4#

Using mathematical induction prove that \(n < 2^n\) holds for all natural numbers \(n=1,2,\dots\).

Verify the statement holds for \(n=1\), and assuming \(n<2^n\) prove that \(n+1 < 2^{n+1}\).

First, we note that for \(n=1\) the statement holds: \(1 < 2^1\). This forms the bases for mathematical induction.

Second, assuming that the statement is true for \(n\), i.e. \(n < 2^n\), we need to prove that it holds for \(n+1\), i.e. \(n+1 < 2^{n+1}\).

  1. multiplying both sides of \(n < 2^n\) by 2 we have \(2n < 2^{n+1}\)

  2. but \(n+1 < 2n\) for all \(n > 1\) because the difference \(2n - (n+1) = n-1\) is always positive for \(n > 1\)

  3. we have \(n+1 < 2n < 2^{n+1}\), therefore taking the leftmost and rightmost inequality we have \(n+1 < 2^{n+1}\)

The first and the second parts together form the base of the induction and the induction step. The statement is therefore true for all \(n=1,2,\dots\). \(\blacksquare\)

\(\alpha\).5#

Let \(A\),\(B\) and \(C\) be any three sets. Show that \(A \cap (B \cup C) = (A\cap B) \cup (A \cap C)\).

One way to show that \(E=F\) is show that a arbitrary element of \(E\) must also be in \(F\) and vice versa.

Let \(A, B\) and \(C\) be any three sets, as in the question. Let

\[ E := A \cap (B \cup C) \quad \text{and} \quad F := (A \cap B) \cup (A \cap C) \]

We need to show that \(E = F\), or, equivalently, that \(E \subset F\) and \(F \subset E\).

To see that \(E \subset F\), pick any \(x \in E\). We claim that \(x \in F\) also holds. To see this, observe that since \(x \in E\), it must be true that \(x\) is in \(A\) as well as being in at least one of \(B\) and \(C\). In the first case \(x\) is in both \(A\) and \(B\). In the second case \(x\) is in both \(A\) and \(C\). In either case we have \(x \in F\) by the definition of \(F\).

To see that \(F \subset E\), pick any \(x \in F\). We claim that \(x \in E\) also holds. Indeed, since \(x \in F\) we know that either \(x\) is in both \(A\) and \(B\) or \(x\) is in both \(A\) and \(C\). In other words, \(x\) is in \(A\) and also at least one of \(B\) and \(C\). Hence \(x \in E\).

\(\alpha\).6#

Find the composition \(g \circ f\) of two functions \(f\) and \(g\), if it exists:

  1. \(f \colon \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x)=\sin(x)\) and \(g \colon \mathbb{R} \rightarrow \mathbb{R}\) defined by \(g(x)= \frac{x}{1+x^2}\)

  2. \(f \colon \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x)= 1-x^4\) and \(g \colon (1,\infty) \rightarrow \mathbb{R}\) defined by \(g(x)= \log(x-1)\)

  3. \(f \colon \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x)=\cos(x)\) and \(g \colon \mathbb{R}\setminus\{1\} \rightarrow \mathbb{R}\) defined by \(g(x)= \frac{x}{1-x}\)

Is there a composition in each case?

The issue we have to deal with is the compatibility of the domains and ranges of the functions.

  1. All good

\[ g \circ f \colon \mathbb{R} \rightarrow \mathbb{R}, \;\; (g \circ f)(x) = \frac{\sin(x)}{1+\sin^2(x)} \]

  1. The range of \(f(x)\) and the domain of \(g(x)\) are disjoint, so the composition is not defined.

  2. The points where \(f(x)=1\) have to be excluded in the composition

\[ g \circ f \colon \mathbb{R}\setminus\{x: \cos(x)=1\} \rightarrow \mathbb{R}, \;\; (g \circ f)(x) = \frac{\cos(x)}{1-\cos(x)} \]

\(\alpha\).7#

For each of the following functions, what is its domain and range? Is it one-to-one? Is it onto? Is it bijective? If it is bijective, write the expression for the inverse function.

  1. \(f(x) = 3x-7\)

  2. \(f(x) = e^x\)

  3. \(f(x) = \ln(x)\)

  4. \(f(x) = \sqrt{x-1}\)

  5. \(f(x) = x^2-1\)

Draw a graph for each function.

  1. \(f(x) = 3x-7\)

  • Domain: \(\mathbb{R}\)

  • Range: \(\mathbb{R}\)

  • One-to-one? Yes

  • Onto? Yes

  • Bijective? Yes

  • Inverse: \(f^{-1}(y) = \frac{y+7}{3}\)

  1. \(f(x) = e^x\)

  • Domain: \(\mathbb{R}\)

  • Range: \(\mathbb{R}_{++} = \{x \in \mathbb{R}: x>0\}\)

  • One-to-one? Yes

  • Onto? No, not on \(\mathbb{R}\), but if we restrict the domain to \(\mathbb{R}_{++}\), then Yes, we can think of \(f(x)\) as a surjection (onto) from \(\mathbb{R}\) to \(\mathbb{R}_{++}\)

  • Bijective? No for \(f(x): \mathbb{R} \to \mathbb{R}\), Yes for \(f(x): \mathbb{R} \to \mathbb{R}_{++}\)

  • Inverse: \(f^{-1}: \mathbb{R}_{++} \ni y \mapsto \ln(y) \in \mathbb{R}\)

  1. \(f(x) = \ln(x)\)

  • Domain: \(\mathbb{R}_{++} = \{x \in \mathbb{R}: x>0\}\)

  • Range: \(\mathbb{R}\)

  • One-to-one? Yes

  • Onto? Yes

  • Bijective? Yes

  • Inverse: \(f^{-1}: \mathbb{R} \ni y \mapsto e^y \in \mathbb{R}_{++}\)

  1. \(f(x) = \sqrt{x-1}\)

  • Domain: \(\mathbb{R}_{+} = [1,\infty) = \{x \in \mathbb{R}: x \ge 1\}\)

  • Range: \(\mathbb{R}_{+}\)

  • One-to-one? Yes

  • Onto? Yes for \(f: \mathbb{R}_{+} \to \mathbb{R}_{+}\)

  • Bijective? Yes

  • Inverse: \(f^{-1}(y) = y^2+1\)

  1. \(f(x) = x^2-1\)

  • Domain: \(\mathbb{R}\)

  • Range: \([-1,\infty) = \{x \in \mathbb{R}: x \ge -1\}\)

  • One-to-one? No

  • Onto? Yes for \(f: \mathbb{R} \to [-1,\infty) \subset \mathbb{R}\), No for \(f: \mathbb{R} \to \mathbb{R}\)

  • Bijective? No because it is not injection (one-to-one)

  • Inverse: undefined because \(f\) is not bijective

Contents