Announcements & Reminders
Tutorials start(ed) this week
Make sure you register for tutorials on course pages
Tutors’ office hours updated on the front page
Reminder on how to ask questions:
Administrative: RSE admin
Content/understanding: tutors
Other: to Fedor
📚 Revision: sets and mappings#
⏱ | words
References and additional materials

Appendix A1.1, 1.2
Chapters 2.1, 2.2, 3.1-3.4, 5.1

Appendix A.1, B.1, B.2
Veritasium video on paradoxes of set theory and mathematical incompleteness YouTube
Notation cheat sheet
Notation |
Meaning |
|---|---|
\(P \implies Q\) |
\(P\) implies \(Q\) |
\(P \iff Q\) |
\(P \implies Q\) and \(Q \implies P\) |
\(\exists\), \(\exists !\) |
there exists, there exists one and only one [element, value] |
\(\forall\) |
for all [elements in a set] |
\(\therefore\) |
therefore [in logical statements] |
\(\because\) |
because [in logical statements] |
\(a \stackrel{def.}{=}\text{[expr]}\) or |
|
\(\in\) |
is element of [a set] |
\(\subset\) |
is subset of [a set] |
\(\cup\) |
union [of sets] |
\(\cap\) |
intersection [of sets] |
Naive set theory#
Definition
A set (\(X\)) is a collection of objects.
A particular object within a set (\(x\)) is known as an element of that set.
Sets: \(A, B, X\)
Elements: \(x,y,z\)
\(x \in X\) denotes the idea that x is an element of X
\(y \notin X\) denotes the idea that y is not an element of X
empty set is denoted by \(\varnothing\)
Definition of a set
A set \(A\) can be defined by either
direct enumeration of its elements
defining a formula for infinite number of elements
as a subset of already defined set \(B\), formula \(\psi(x)\) to form elements of \(A\), and a condition/property on \(x\)
Russell’s Paradox
Let \(\mathbb{A}\) be the property “is a set and does not belong to itself”. Suppose that \(A\) is the set of all sets that possess property \(\mathbb{A}\). Is \(A \in A\)?
– Bertrand Russell, 1901
If \(A \in A\), then it must be the case that \(A\) possesses property \(\mathbb{A}\). This means that \(A \notin A\). Contradiction! Thus it must be the case that \(A \notin A\). But if \(A\) is a set and \(A \notin A\), then it clearly possesses property \(\mathbb{A}\). Thus \(A \in A\). Contradiction. Thus it must be the case that \(A \in A\).
We have a paradox. It cannot be the case that both \(A \in A\) and \(A \notin A\).
One possible resolution to Russell’s paradox is to not allow mathematical objects like this particular \(A\) to be considered a set. Re-definition of the set theory by Ernst Zermelo, Abraham Fraenkel and Thoralf Skolem in 1908-1920, known today as ZFC axiomatic set theory.
Definition
Consider two sets, \(X\) and \(Y\). Suppose that every element of \(X\) also belongs to \(Y\). If this is the case, then we say that \(X\) is a subset of \(Y\).
This is written in mathematical notation as \(X \subseteq Y\).
Definition
Suppose that in addition to every element of \(X\) also belonging to \(Y\), there is at least one element of Y that does not belong to \(X\). If this is the case, then we say that \(X\) is a proper subset of \(Y\).
Definition
The power set \(2^X\) of a set \(X\) is the set of all subsets of \(X\).
Note that the elements of a power set are sets themselves.
Example
Suppose that \(X = \{1, 2, 3\}\). The power set for the set \(X\) in this example is
Definition
The Cartesian product of two sets is defined to be the set of all ordered pairs (or doublets) that contain one component from each of the two sets in the order that the sets were specified. This can be formally expressed as
Definition
The Cartesian product of \(n\) sets is defined to be the set of all ordered \(n\)-tuples that contain one component from each of the \(n\) sets in the order that the sets were specified. This can be formally expressed as
Note that the order of the sets matters here. Cartesian products generate sets of “ordered” n-tuples.
Operations on sets#
Definition
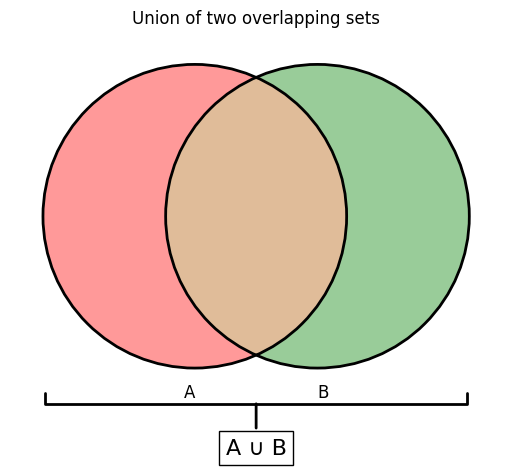
The union of \(X\) and \(Y\), which is denoted by \(X \cup Y\), is the set
Definition
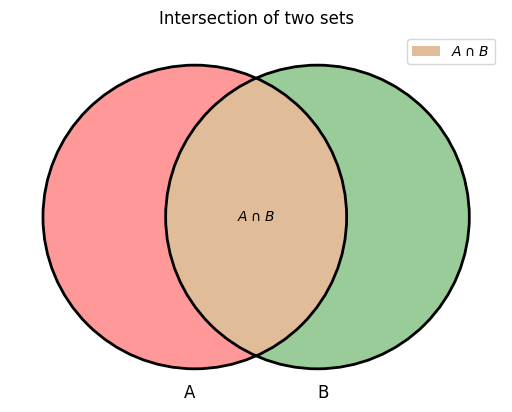
The intersection of \(X\) and \(Y\), which is denoted by \(X \cap Y\), is the set
Definition
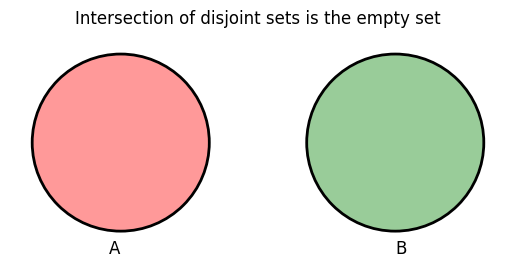
If \(X \cap Y = \varnothing\), then the sets \(X\) and \(Y\) are said to be disjoint.
Definition
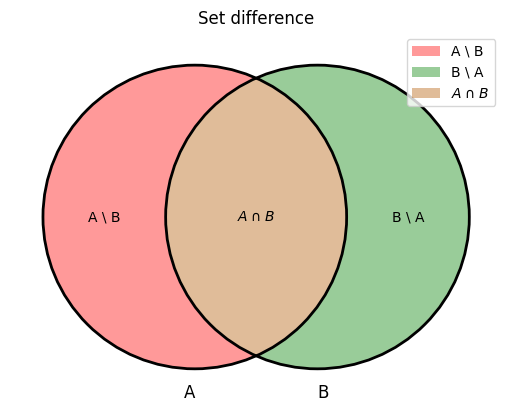
The set difference “X excluding Y”, which is denoted by \(X \setminus Y\), is the set
Definition
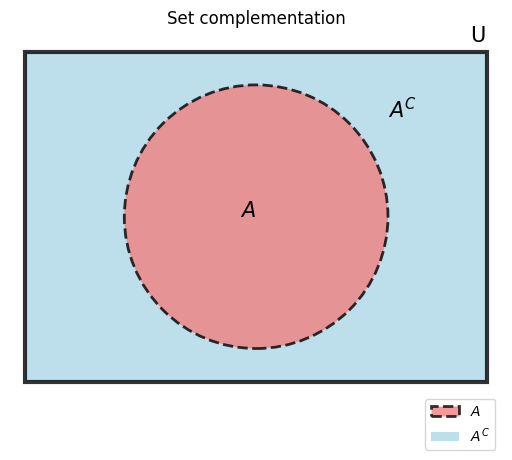
Set complementation is a special case of set exclusion. The complement of the set \(X\), which is denoted by \(X^C\) , is defined as \(X^C = U \setminus X\).
Note
There are several alternative notations for the complement of a set, including \(X^C\), \(X'\), \(\bar{X}\), and \(\neg X\).
Note that \(X \cup X^C = U\) and \(X \cap X^C = \varnothing\).
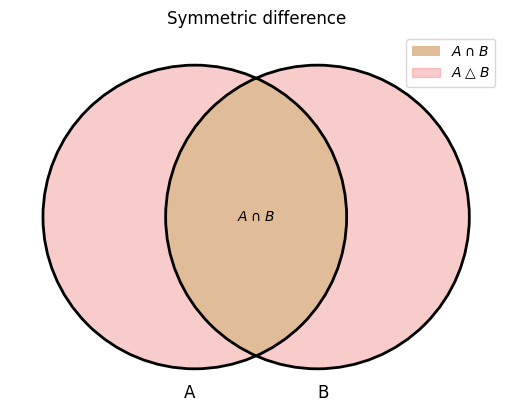
Definition
The symmetric difference of \(X\) and \(Y\), which is denoted by \(X \bigtriangleup Y\), is the set
Note
Exclusive or is another name for the symmetric difference operation.
Sets of numbers#
The set of natural numbers \(\mathbb{N} = \{1, 2, 3, · · · \}\)
The set of integer \(\mathbb{Z} = \{· · · , −2, −1, 0, 1, 2, · · · \}\)
The set of rational number \(\mathbb{Q} = \{ \frac{m}{n} : m \in \mathbb{Z}, n \in \mathbb{N}\}\)
The set of real numbers \(\mathbb{R} = (-\infty, \infty)\)
The set of non-negative real numbers \(\mathbb{R}_+ = \{x \in \mathbb{R} : x \geqslant 0\} = [0, \infty)\)
The set of positive real numbers \(\mathbb{R}_{++} = \{x \in \mathbb{R}: x > 0\} = (0, \infty)\)
The set of complex numbers \(\mathbb{C} = \{ a + bi : a \in \mathbb{R}, \: b \in \mathbb{R}, \: i = \sqrt{−1} \}\)
Example
The following “nesting” relationship exists between these common sets of numbers:
Let \(a \in \mathbb{R}, b \in \mathbb{R} \text{ and } a < b\). There are four types of intervals of an interval:
\([a, b] = \{x \in \mathbb{R} : a \leqslant x \leqslant b\}\)
\((a, b) = \{x \in \mathbb{R} : a < x < b\}\)
\([a, b) = \{x \in \mathbb{R} : a \leqslant x < b\}\)
\((a, b] = \{x \in \mathbb{R} : a < x \leqslant b\}\)
Multidimensional number sets (with vectors as elements) are given by Cartesian products
The \(n\)-dimensional Euclidean coordinate plane:
The real number system#
There are several approaches for defining rigorously what numbers are:
axiomatic approach (real numbers are something that )
model-theoretic approach (Dedekind cuts, etc)
Axiomatic definition#
Definition
A field is a set of numbers that is closed under addition, subtraction, multiplication, and division (except by zero element).
“closed” means that any two elements in the field can be added, subtracted, multiplied, and divided (except by zero) to produce another element in the field
field is one of many abstract algebraic structures (such as groups, rings, lattices, algebras, etc) which are axiomatically defined by imposing specific properties on the set and its operations between its elements
Definition
An ordered field is a field that is also equipped with a total order relation that is compatible with the field operations.
every pair of elements in the total order can be compared
Example
The set of rational numbers \(\mathbb{Q}\) is an ordered field.
Definition
A complete field is a field in which every non-empty subset that is bounded above has a least upper bound (which belongs to the field).
this property is known as the completeness axiom and can be stated in several different equivalent ways:
through infinite series of nested intervals (Cantor’s intersection theorem)
through limits of monotone sequences (details later in the course)
through convergence of Cauchy sequences (details later in the course)
it does not hold for the set of rational numbers \(\mathbb{Q}\): for example, the set of rational numbers each element of which squared is is less than \(2\) has no least upper bound in \(\mathbb{Q}\)
Definition
Real numbers \(\mathbb{R}\) are defined as a complete ordered field.
completeness ensures that the real number line has no gaps in it
unlike the rational numbers!
Fact
\(\sqrt{2}\) is not a rational number.
Proof
We can prove this proposition by contradiction.
Assume that \(\sqrt{2} = \frac{p}{q}\) where \(p\) ad \(q\) are whole numbers.
Without loss of generality we can choose \(p\) and \(q\) such that they do not have common factors, otherwise these factors can be cancelled out.
Then \(\frac{p^2}{q^2} = 2\), and so \(2q^2 = p^2 \iff p^2\) is a multiple of 2.
All components in prime decomposition of \(p^2\) enter in pairs because it is a square, therefore there must be an even number of 2’s in the factorization of \(p^2\) \(\implies\) \(p\) is a multiple of 2 itself.
Therefore we can find a whole number \(r\) such that \(p = 2r\), and substitute to get \(2q^2 = 4r^2 \implies q^2 = 2r^2\).
Now the same arguments applied to \(q\) let us conclude that \(q\) is also a multiple of 2.
This contradicts our choice of \(p\) and \(q\) not having common factors!
Therefore our assumption that \(\sqrt{2} = \frac{p}{q}\) is false, and thus \(\sqrt{2}\) is indeed an irrational number. \(\blacksquare\)
however, \(\sqrt{2}\) is a very “real” number which we encounter in many practical situations: diagonal of a square with side length 1 meter
What’s next?#
rigorous definitions of number representation
decimal representation
continued fractions
rigorous definitions of algebraic operations
addition
subtraction
multiplication
division
rigorous definitions of order relations
less than
greater than
less than or equal to
greater than or equal to
rigorous definitions of convergence and limits
etc.
This is re-definition of all our “common sense” knowledge about numbers in a rigorous mathematical language \(\implies\) we can use standard arithmetic operations at a deeper level of mathematical rigour.
Dedekind cuts#
theoretical model of real numbers
allows for rigorous definition of real numbers in a constructive way without relying on the axioms
associates a real number to a set (rather, two sets forming a partition of another set)
Definition
A Dedekind cut is a partition of the rational numbers into two non-empty sets \(A\) and \(A'\) such that
every rational number is in either \(A\) or \(A'\), but not in both
every element of \(A\) is less than every element of \(A'\)
The set \(A\) is referred to as lower half, the set \(A'\) as upper half.
Examples of Dedekind cuts
\(A \subset \mathbb{Q}: \forall a \in A \:\: a < 1\), \(A' \subset \mathbb{Q}: \forall a' \in A' \:\: a' \ge 1\)
\(A \subset \mathbb{Q}: \forall a \in A \:\: a \le 1\), \(A' \subset \mathbb{Q}: \forall a' \in A' \:\: a' > 1\)
\(A \subset \mathbb{Q}: \forall a \in A \:\: a^2 < 2\), \(A' \subset \mathbb{Q}: \forall a' \in A' \:\: a'^2 > 2\)
Fact
The above three examples cover all possible cases for Dedekind cuts:
Upper half has the least element
Lower half has the greatest element
Neither half has the least or the greatest element
Proof
It is easy to show that it is impossible that both \(A\) has the greatest and \(A'\) has the least element. If it was possible, than there would be a rational number at midpoint between these two elements which would not belong to either \(A\) and \(A'\), which is a contradiction.
Let’s prove the third example case, namely that \(A\) has no greatest element (the absence of least element in \(A'\) is proven analogously). Consider any \(a \in A\), we have \(a^2<2\). We can show that there exists a natural number \(n \in \mathbb{N}\) such that
and therefore \(a+1/n \in A\). Indeed, the last inequality is equivalent to
The last inequality holds true if we impose \(\tfrac{2a+1}{n} < 2 - a^2\), therefore choosing \(n\) to satisfy
ensures that \(a + 1/n \in A\).
Thus, for any \(a \in A\) we can find a greater element \(a + 1/n \in A\), and therefore \(A\) has no greatest element. \(\blacksquare\)
Definition
Dedekind cut of the third type (those which do not have the least element in the upper half and the greatest element in the lower half) defines an irrational number.

irrational numbers are objects of new type, they are not rational numbers by construction
fill in the “holes” between rational numbers
rational numbers \(\mathbb{Q}\) and irrational numbers defined by Dedekind cuts form the set of real numbers \(\mathbb{R}\)
Fact
For any real numbers \(a,b \in \mathbb{R}\) where \(a>b\) there is a real number \(c \in \mathbb{R}\) such that \(b<c<a\).
Proof
Denote \(A|A'\) and \(B|B'\) the Dedekind cuts corresponding to \(a\) and \(b\) respectively.
Because \(a>b\), we have \(B \subset A\) yet \(B \ne A\). Thus, there exists a rational number \(c \in A \setminus B\).
We have \(c \in A\), that is \(c<a\). But \(c \notin B\), it follows that \(c \in B'\), and therefore \(c>b\)
Thus, \(b<c<a\). \(\blacksquare\)
it follows from the proof that the number \(c\) is in fact rational
it also follows by repeated application of the proposition that an infinite number of rational numbers can be fitted between any two given rational numbers, however close they are in the number line
overall, the number line of real numbers has no gaps!
What’s next?#
Same steps as in axiomatic approach to define the common sense operations, but using Dedekind cuts as the definition of real numbers.
rigorous definitions of number representation using Dedekind cuts
decimal representation
continued fractions
rigorous definitions of algebraic operations using Dedekind cuts
addition
subtraction
multiplication
division
rigorous definitions of order relations from set theory
less than
greater than
less than or equal to
greater than or equal to
rigorous definitions of convergence and limits
etc.
This is re-definition of all our “common sense” knowledge about numbers in a rigorous mathematical language \(\implies\) we can use standard arithmetic operations at a deeper level of mathematical rigour.
Example
Note
Division by zero in not defined for any real number \(p\).
Note
When exponent is fractional and base is negative, the result is undefined for non-integer exponents.
See discussion here
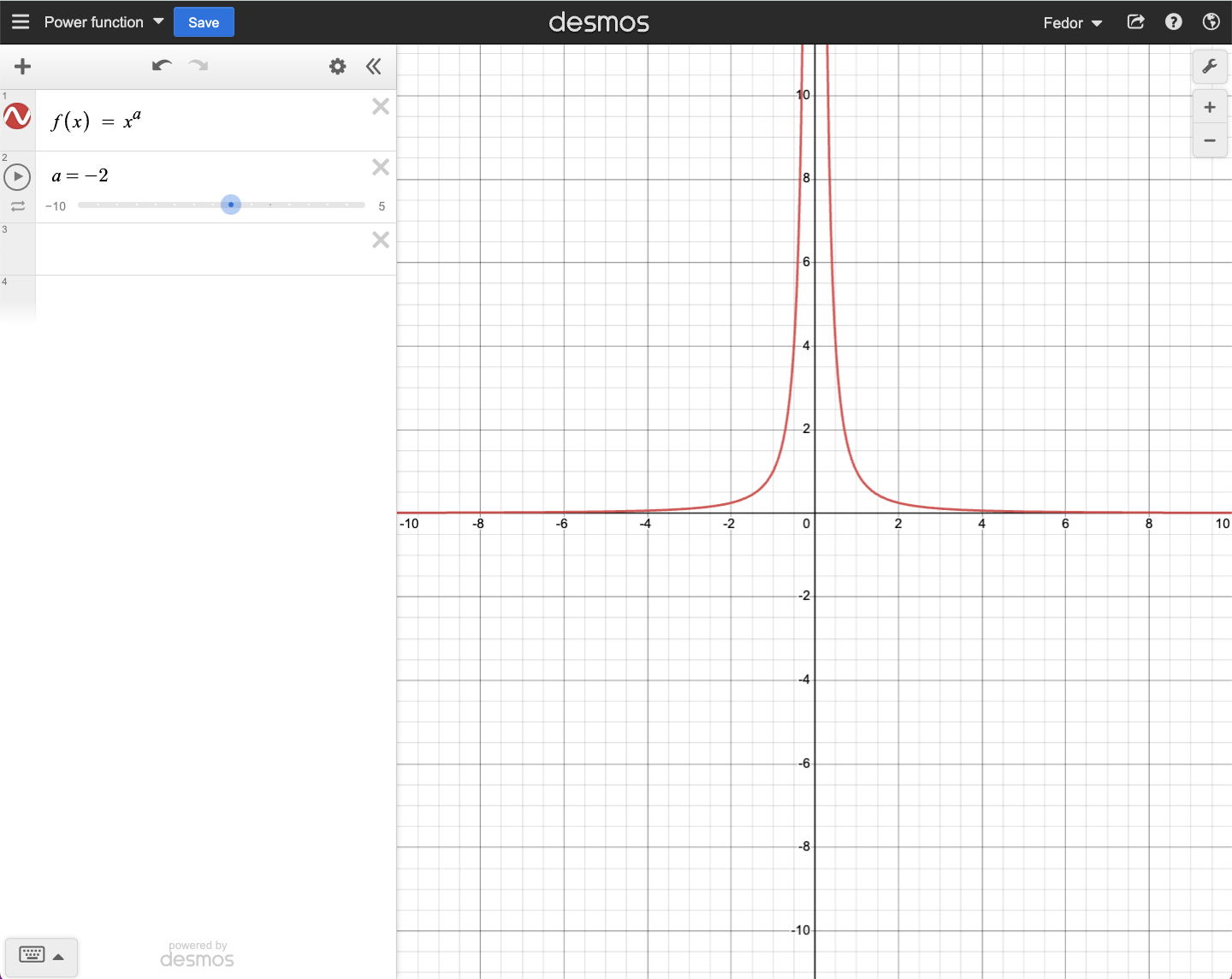
Functions and other mappings#
Definition
A generic mapping \(f\) from \(A\) to \(B\) is a rule that assigns elements \(x\) of a set \(A\) to elements of a set \(B\). We write
Definition
A function \(f: A \rightarrow B\) from set \(A\) to set \(B\) is a mapping that associates to each element of \(A\) a uniquely determined element of \(B\).
Definition
\(A\) is called the domain of \(f\) and \(B\) is called the co-domain
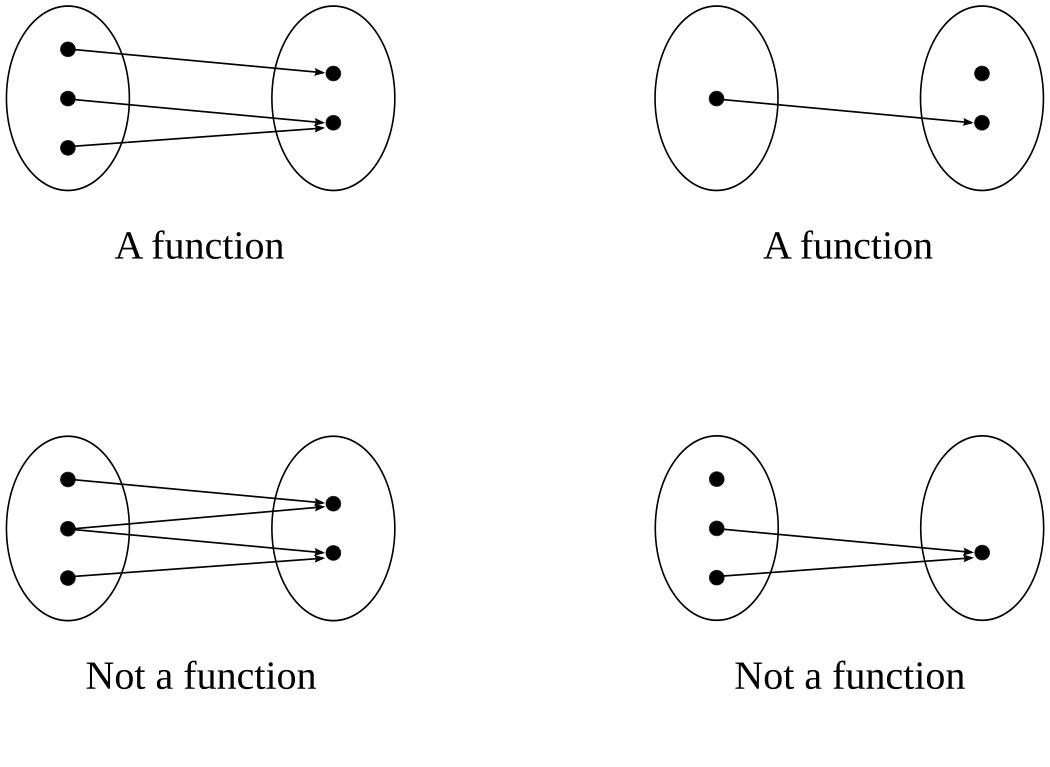
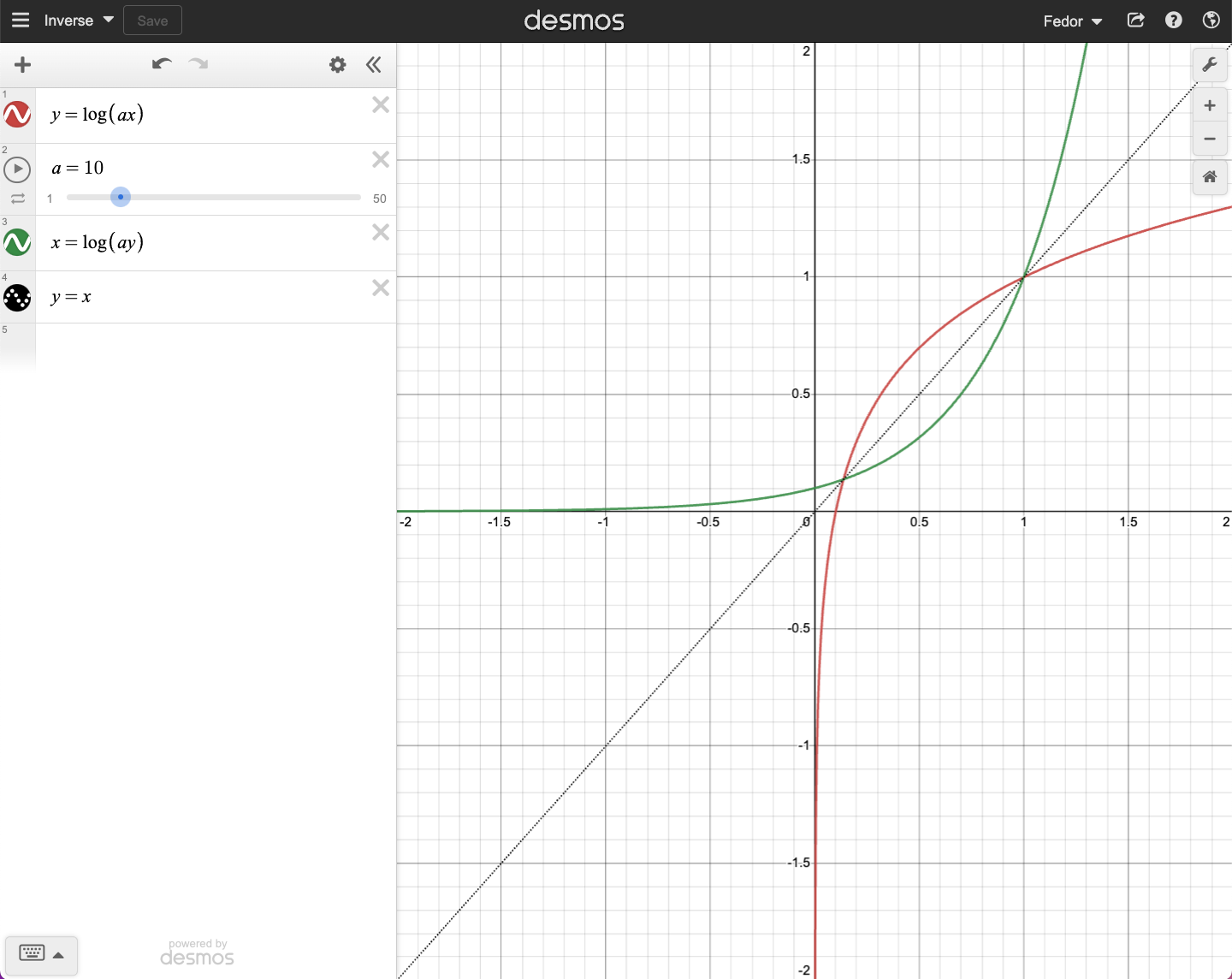
Example
Consider the sets \(A=\{a,b,c,d\}\) and \(B=\{1,2,3,4\}\). The following diagrams illustrate possible associations between elements of \(A\) and \(B\), i.e. domain \(A\) and co-domain \(B\):
These associations can be written as subsets of the Cartesian product \(A \times B\) as follows:
(i) \(\{(a,2),(b,1),(c,4),(d,4)\} \subset A \times B\)
(ii) \(\{(a,1),(a,2),(b,3),(c,4)\} \subset A \times B\)
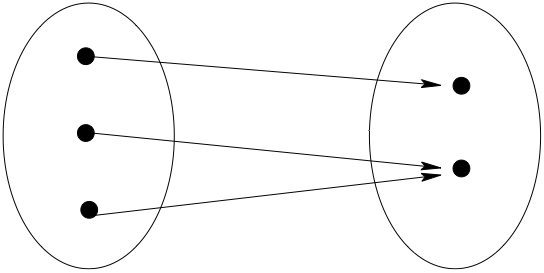
Panel (i) illustrates a function from \(A\) to \(B\) because each element of \(A\) is associated with no more than one element of \(B\).
Panel (ii) does not illustrate a function from \(A\) to \(B\) because the element \(a\) is associated with two elements of \(B\), and element \(d\) is not associated with any element of \(B\).
Definition
Functions can be:
scalar-valued when \(n=1\), so \(f: A \to \mathbb{R}\)
vector-valued when \(n>1\), so \(f: A \to \mathbb{R}^n\)
univariate when \(A = \mathbb{R}\), so \(f: \mathbb{R} \to \mathbb{R}^n\)
multivariate when \(A = \mathbb{R}^m\), so \(f: \mathbb{R}^m \to \mathbb{R}^n\)
Definition
For each \(a \in A\), \(f(a) \in B\) is called the image of \(a\) under \(f\)
Definition
If \(f(a) = b\) then \(a\) is called a pre-image of \(b\) under \(f\)
Definition
The definitions of image and pre-image naturally generalize to subsets of the domain.
For each \(X \subset A\), \(f(X) = \{f(x): x \in X\} \in B\) is called the image of \(X\) under \(f\)
For each \(Y \subset B\), \(\{x: f(x) \in Y\} \in A\) is called the pre-image of \(Y\) under \(f\)
Definition
The smallest possible co-domain is called the range of \(f: A \to B\):
Definition
The composition of \(f: A \to B\) and \(g: B \to C\) is the function \(g \circ f\) from \(A\) to \(C\) defined by
Surjection, injection and bijection#
Definition
A function \(f: A \to B\) is called onto (or surjection) if every element of \(B\) is the image under \(f\) of at least one point in \(A\).
Equivalently, \(\mathrm{rng}(f) = B\)
Fact
\(f: A \to B\) is onto if and only if each element of \(B\) has at least one pre-image under \(f\)
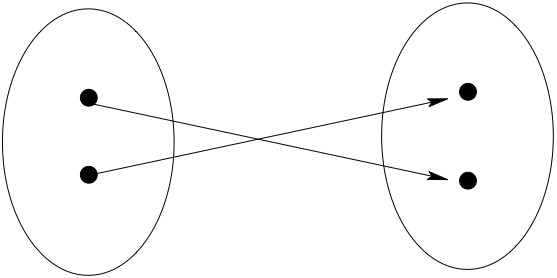
Fig. 1 Onto (surjection)#
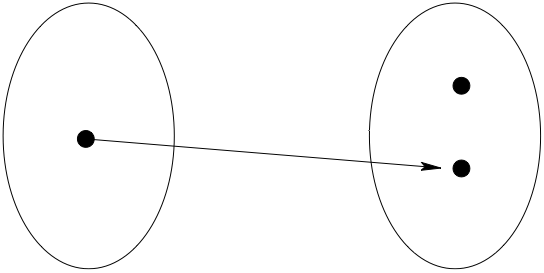
Fig. 2 Not onto!#
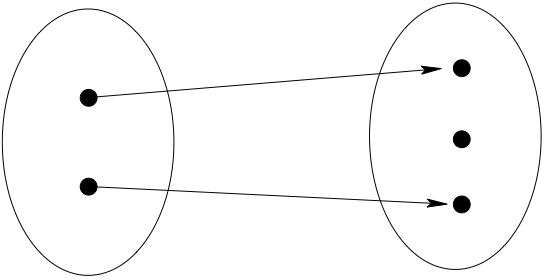
Fig. 3 Not onto!#
Definition
A function \(f: A \to B\) is called one-to-one (or injection) if distinct elements of \(A\) are always mapped into distinct elements of \(B\).
That is, \(f\) is one-to-one if
Equivalently,
Fact
\(f: A \to B\) is one-to-one if and only if each element of \(B\) has at most one pre-image under \(f\)

Fig. 4 One-to-one#

Fig. 5 One-to-one#
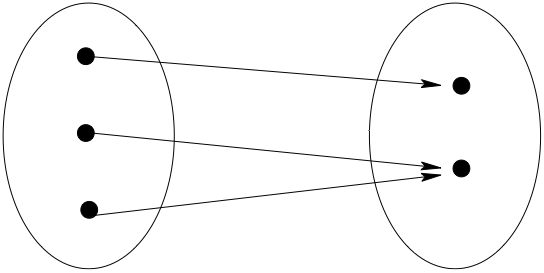
Fig. 6 Not one-to-one#
Definition
A function that is
one-to-one (injection) and
onto (surjection)
is called a bijection or one-to-one correspondence

Fact
\(f: A \to B\) is a bijection if and only if each \(b \in B\) has one and only one pre-image in \(A\)
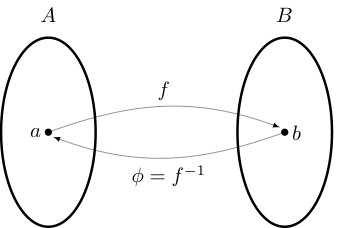
Fact
If \(f: A \to B\) a bijection, then there exists a unique function \(\phi: B \to A\) such that
That function \(\phi\) is called the inverse of \(f\) and written \(f^{-1}\)
Fact
If \(f: A \to B\) is one-to-one, then \(f: A \to \mathrm{rng}(f)\) is a bijection
Fact
Let \(f: A \to B\) and \(g: B \to C\) be bijections
\(f^{-1}\) is a bijection and its inverse is \(f\)
\(f^{-1}(f(a)) = a\) for all \(a \in A\)
\(f(f^{-1}(b)) = b\) for all \(b \in B\)
\(g \circ f\) is a bijection from \(A\) to \(C\) and \((g \circ f)^{-1} = f^{-1} \circ g^{-1}\)
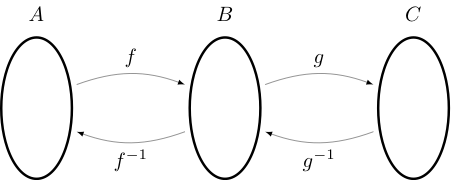
Fig. 7 Illustration of \((g \circ f)^{-1} = f^{-1} \circ g^{-1}\)#
Monotonicity#
Definition
A function \(f : X \rightarrow \mathbb{R}\), where \(X \subseteq \mathbb{R}\), is said to be a non-decreasing function if
Definition
A function \(f : X \rightarrow \mathbb{R}\), where \(X \subseteq \mathbb{R}\), is said to be a strictly increasing function if both
(a) \(x = y \iff f(x) = f(y)\); and
(b) \(x < y \iff f(x) < f(y)\).
Definition
Non-increasing and strictly decreasing functions are defined in a similar manner, with the inequality signs flipped.
Definition
Monotonic transformation of a given function is its composition with a a strictly increasing or strictly decreasing function.
Graphs#
Definition
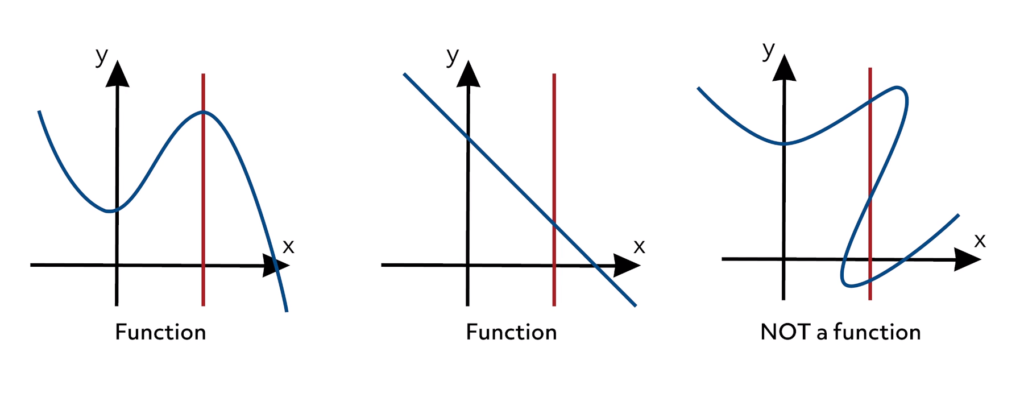
A graph of a mapping \(f \colon X \to Y\) is a set \(\Gamma \subset X \times Y\) of points \(x \in X\) and \(y \in Y\) where it holds \(y \in f(x)\), or \(y = f(x)\) in the case \(f\) is a function.
Fact
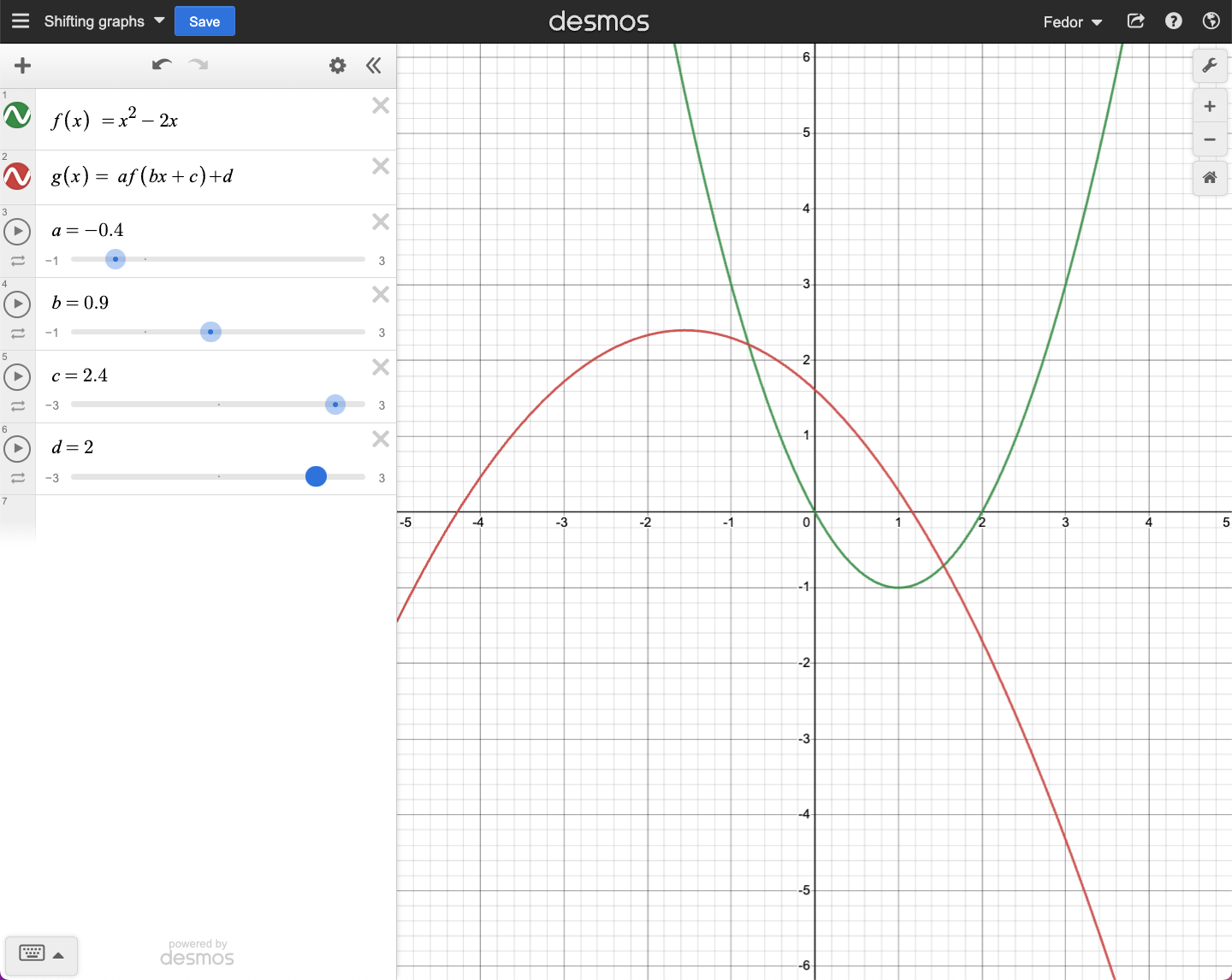
Consider \(\Gamma_0\) the graph of function \(f(x): \mathbb{R} \to \mathbb{R}\). Denote \(\Gamma_1\) the graph of the composite function \(g(x) = af(bx+c)+d\), such that when \(a=b=1\) and \(c=d=0\) \(f(x)=g(x)\). It holds that:
for \(a \ne 1\), \(a>0\) graph \(\Gamma_1\) is a vertical stretch or compression of \(\Gamma_0\) by a factor of \(|a|\)
for \(a<0\) in addition graph \(\Gamma_1\) flips around the horizontal axis
for \(b \ne 1\), \(b>0\) graph \(\Gamma_1\) is a horizontal stretch or compression of \(\Gamma_0\) by a factor of \(|b|\)
for \(b<0\) in addition graph \(\Gamma_1\) flips around the vertical axis
for \(c \ne 0\) graph \(\Gamma_1\) is a horizontal shift of \(\Gamma_0\) by \(\frac{c}{b}\), left for \(\frac{c}{b}>0\) and right for \(\frac{c}{b}<0\)
for \(d \ne 0\) graph \(\Gamma_1\) is a vertical shift of \(\Gamma_0\) by \(d\), up for \(d>0\) and down for \(d<0\)
Fact
When the inverse exists, its graph is a flip of the original graph over the 45 degree line.
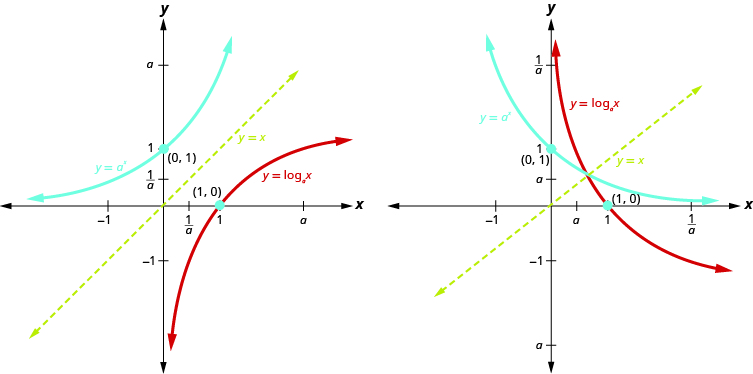
Fig. 10 Graph of inverse functions#
Cardinality#
Definition
If a bijection exists between sets \(A\) and \(B\) they are said to have the same cardinality, and we write \(|A| = |B|\)
Fact
If \(|A| = |B|\) and \(A\) and \(B\) are finite then \(A\) and \(B\) have the same number of elements (same cardinality).
Hence “same cardinality” is analogous to “same size”
Definition
The number of elements of finite set \(X\) is called the cardinality of \(X\), and is denoted by any of the following notation:
\(\lvert X \rvert\)
\(\# X\)
\(nX\)
\(n(X)\)
General rule
Example
What is the number of elements of \(A \cup B\), \(|A \cup B|\)?
But!
It depends on whether \(A\) and \(B\) are disjoint or not!
Fact
If \(A_n\) are finite for \(n=1, \ldots,N\), then
That is, number of possible tuples \(=\) product of the number of possibilities for each element
Example
Number of binary sequences of length \(10\) is
But cardinality applies to infinite sets as well!
Fact
If \(|A| = |B|\) and \(|B| = |C|\) then \(|A| = |C|\)
Proof
Since \(|A| = |B|\), there exists a bijection \(f: A \to B\)
Since \(|B| = |C|\), there exists a bijection \(g: B \to C\)
Let \(h := g \circ f\)
Then \(h\) is a bijection from \(A\) to \(C\)
Hence \(|A| = |C|\)
Definition
A nonempty set \(A\) is called finite if
Otherwise called infinite
Definition
Sets that either are finite, or have the same cardinality as \(\mathbb{N}\), denoted \(|A| = \aleph_0\), are called countable
Fact
A set \(X\) countable if and only if there exists a bijection \(f: X \rightarrow \mathbb{N}\).
Example
\(-\mathbb{N} := \{\ldots, -4, -3, -2, -1\}\) is countable
Formally: \(f(k) = -k\) is a bijection from \(-\mathbb{N}\) to \(\mathbb{N}\)
Example
\(E := \{2,4,6, \ldots\}\) is countable
Formally: \(f(k) = k/2\) is a bijection from \(E\) to \(\mathbb{N}\)
Fact
Nonempty subsets of countable sets are countable
Fact
Finite unions of countable sets are countable
Proof
Sketch of proof for \(A\) and \(B\) countable \(\implies A \cup B\) countable.
Consider \(A\) and \(B\) are disjoint and infinite (the most complicated case)
By assumption, can write \(A = \{a_1, a_2, \ldots\}\) and \(B = \{b_1, b_2, \ldots\}\)
Now count it like so:
Example
\(\mathbb{Z} = \{\ldots, -2, -1\} \cup \{ 0 \} \cup \{1, 2, \ldots\}\) is countable
Fact
Finite Cartesian products of countable sets is countable
Proof
Sketch of proof for \(A\) and \(B\) countable \(\implies A \times B\) countable.
Consider \(A\) and \(B\) are disjoint and infinite (the most complicated case). Now count like so:
Example
\(\mathbb{Z} \times \mathbb{Z} = \{ (p,q) : p \in \mathbb{Z}, q \in \mathbb{Z} \}\) is countable
Fact
\(\mathbb{Q}\) is countable
Proof
By definition
Consider the function \(\phi\) defined by \(\phi(p/q) = (p, q)\)
A one-to-one function from \(\mathbb{Q}\) to \(\mathbb{Z} \times \mathbb{N}\)
A bijection from \(\mathbb{Q}\) to \(\mathrm{rng}(\phi)\)
Since \(\mathbb{Z} \times \mathbb{N}\) is countable, so is \(\mathrm{rng}(\phi) \subset \mathbb{Z} \times \mathbb{N}\)
Hence \(\mathbb{Q}\) is also countable
Example
An example of an uncountable set is all binary sequences
Proof
Sketch of proof by contradiction. If this set were countable then it could be listed as follows:
Consider a sequence that dffers from \({a_k}\) in the first element, from \({b_k}\) in the second element, from \({c_k}\) in the third element, and so on. This sequence is not in the list, hence the list is incomplete. Contradition \(\implies\) the set of infinite binary sequences is not countable.
Fact
Such a list is never complete: Cantor’s diagonalization argument
Cardinality of \(\{0,1\}^{\mathbb{N}}\) called the power of the continuum
Other sets with the power of the continuum
\(\mathbb{R}\)
\((a, b)\) for any \(a < b\)
\([a, b]\) for any \(a < b\)
\(\mathbb{R}^N\) for any finite \(N \in \mathbb{N}\)
Continuum hypothesis
Every nonempty subset of \(\mathbb{R}\) is either countable or has the power of the continuum
Example
\(\mathbb{R}\) and \((-1, 1)\) have the same cardinality because \(x \mapsto 2\arctan(x)/\pi\) is a bijection from \(\mathbb{R}\) to \((-1, 1)\)
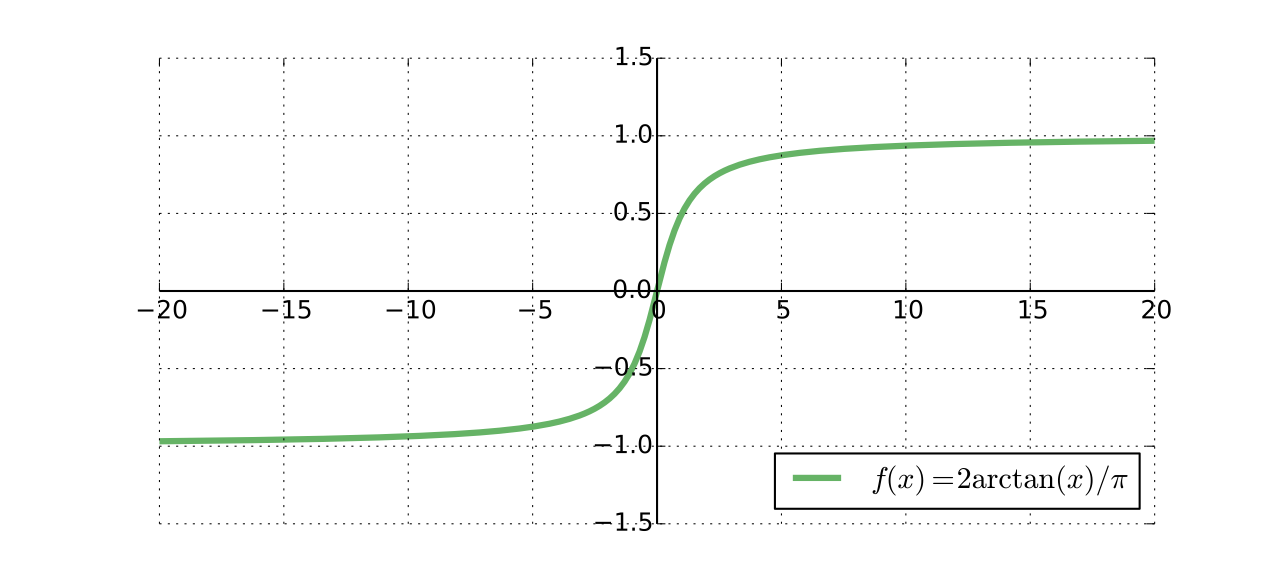
Fig. 11 Same cardinality#