Announcements & Reminders
We start today with the revision of convergence and limits in this lecture before moving on to today’s lecture, so have a busy agenda
The issue with the tutorial schedule has been brought up (thank you!) and resolved: there will be tutorial on Monday as scheduled, the schedule in these notes is now updated
Next week Monday March 10 is public holiday, the lectures will be recorded, links posted on this website
This week we have the first online test, scheduled for Sunday March 9
I usually schedule online test for a day before the lecture to give you maximum time to prepare
However this is Sunday this semester
How do people feel about taking the tes on Sunday?
Please, vote on Wattle page before noon tomorrow March 4
📚 Revision: sequences and limits#
⏱ | words
References and additional materials
Review of the basics of real analysis (mathematical analysis studies sequences, limit, continuity, differentiation, integration, etc.)
Note
Many textbooks use bold notation for vectors, but we do not. Typically it is explicitly stated that \(x \in \mathbb{R}^n\).
Norm and distance#
Recall that multidimensional number sets (with vectors as elements) are given by Cartesian products
Definition
The (Euclidean) norm of \(x \in \mathbb{R}^n\) is defined as
\(\| x \|\) represents the length of \(x\)

Fig. 12 Length of red line \(= \sqrt{x_1^2 + x_2^2} =: \|x\|\)#
\(\| x - y \|\) represents distance between \(x\) and \(y\)
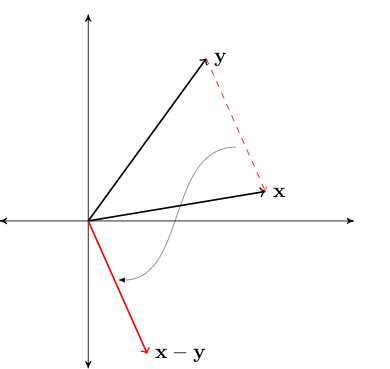
Fig. 13 Length of red line \(= \|x - y\|\)#
Fact
For any \(\alpha \in \mathbb{R}\) and any \(x, y \in \mathbb{R}^n\), the following statements are true:
\(\| x \| \geq 0\)
\(\| x \| = 0 \iff x = 0\)
\(\| \alpha x \| = |\alpha| \| x \|\)
Triangle inequality
\(\| x + y \| \leq \| x \| + \| y \|\)
Proof
For example, let’s show that \(\| x \| = 0 \iff x = 0\)
First let’s assume that \(\| x \| = 0\) and show \(x = 0\)
Since \(\| x \| = 0\) we have \(\| x \|^2 = 0\) and hence \(\sum_{i=1}^n x_i^2 = 0\)
That is \(x_i = 0\) for all \(i\), or, equivalently, \(x = 0\)
Next let’s assume that \(x = 0\) and show \(\| x \| = 0\)
This is immediate from the definition of the norm.
\(\blacksquare\)
In fact, any function can be used as a norm, provided that the listed properties are satisfied
Example
More general distance function in \(\mathbb{R}\).
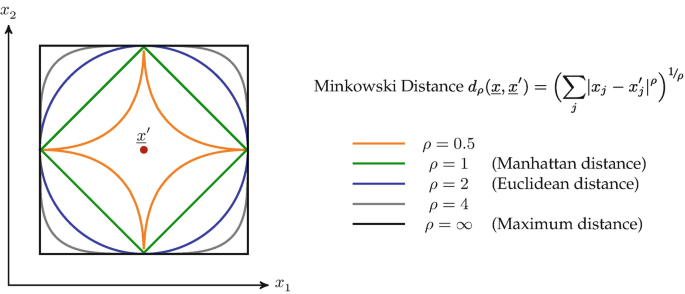
Fig. 14 Circle drawn with different norms#
Example
Naturally, in \(\mathbb{R}\) Euclidean norm simplifies to
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
def subplots():
"Custom subplots with axes throught the origin"
fig, ax = plt.subplots()
# Set the axes through the origin
for spine in ['left', 'bottom']:
ax.spines[spine].set_position('zero')
for spine in ['right', 'top']:
ax.spines[spine].set_color('none')
ax.grid()
return fig, ax
fig, ax = subplots()
ax.set_ylim(-3, 3)
ax.set_yticks((-3, -2, -1, 1, 2, 3))
x = np.linspace(-3, 3, 100)
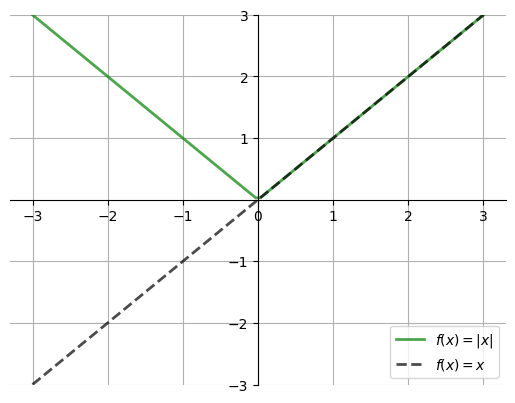
ax.plot(x, np.abs(x), 'g-', lw=2, alpha=0.7, label=r'$f(x) = |x|$')
ax.plot(x, x, 'k--', lw=2, alpha=0.7, label=r'$f(x) = x$')
ax.legend(loc='lower right')
plt.show()
Therefore we can think of norm as a generalization of the absolute value to \(\mathbb{R}\)
\(\epsilon\)-balls#
Definition
For \(\epsilon > 0\), the \(\epsilon\)-ball \(B_{\epsilon}(a)\) around \(a \in \mathbb{R}^n\) is the set of all \(x \in \mathbb{R}^n\) such that \(\|a - x\| < \epsilon\)
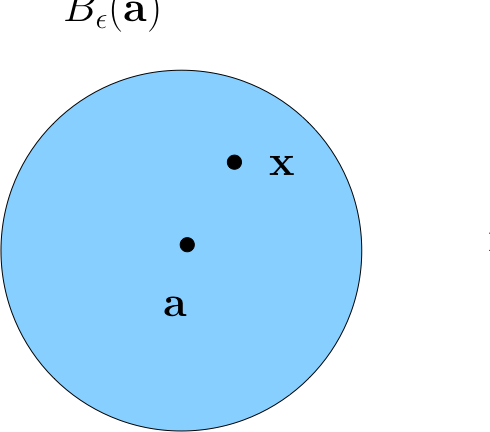
Correspondingly, in one dimension \(\mathbb{R}\)

The following fact is an alternative way to refer to the completeness of \(\mathbb{R}\), see previous lecture on density of real numbers.
Fact
If \(x\) is in every \(\epsilon\)-ball around \(a\) then \(x=a\)
Proof
Suppose to the contrary that
\(x\) is in every \(\epsilon\)-ball around \(a\) and yet \(x \ne a\)
Since \(x\) is not \(a\) we must have \(\|x-a\| > 0\)
Set \(\epsilon := \|x-a\|\)
Since \(\epsilon > 0\), we have \(x \in B_{\epsilon}(a)\)
This means that \(\|x-a\| < \epsilon\)
That is, \(\|x - a\| < \|x - a\|\)
Contradiction!
\(\blacksquare\)
Fact
If \(a \ne b\), then \(\exists \; \epsilon > 0\) such that \(B_{\epsilon}(a)\) and \(B_{\epsilon}(b)\) are disjoint.

Proof
Let \(a, b \in \mathbb{R}^n\) with \(a \ne b\)
If we set \(\epsilon := \|a-b\|/2\), then \(B_{\epsilon}(a)\) and \(B_\epsilon(b)\) are disjoint
To see this, suppose to the contrary that \(\exists \, x \in B_{\epsilon}(a) \cap B_\epsilon(B)\)
Then \( \|x - a\| < \|a -b\|/2\) and \(\|x - b\| < \|a -b\|/2\)
But then
Contradiction!
\(\blacksquare\)
Sequences#
Definition
A sequence \(\{x_k\}\) in \(\mathbb{R}^n\) is a function from \(\mathbb{N}\) to \(\mathbb{R}^n\)
To each \(n \in \mathbb{N}\) we associate one \(x_k \in \mathbb{R}^n\)
Typically written as \(\{x_k\}_{k=1}^{\infty}\) or \(\{x_k\}\) or \(\{x_1, x_2, x_3, \ldots\}\)
Example
In \(\mathbb{R}\)
\(\{x_k\} = \{2, 4, 6, \ldots \}\)
\(\{x_k\} = \{1, 1/2, 1/4, \ldots \}\)
\(\{x_k\} = \{1, -1, 1, -1, \ldots \}\)
\(\{x_k\} = \{0, 0, 0, \ldots \}\)
In \(\mathbb{R}^n\)
\(\{x_k\} = \big\{(2,..,2), (4,..,4), (6,..,6), \ldots \big\}\)
\(\{x_k\} = \big\{(1, 1/2), (1/2,1/4), (1/4,1/8), \ldots \big\}\)
Definition
Sequence \(\{x_k\}\) is called bounded if \(\exists M\in \mathbb{R}\) such that \(\|x_k\| < M\) for all \(k\)x.
Example
Convergence and limit#
\(\mathbb{R}^1\)#
Let \(a \in \mathbb{R}\) and let \(\{x_k\}\) be a sequence
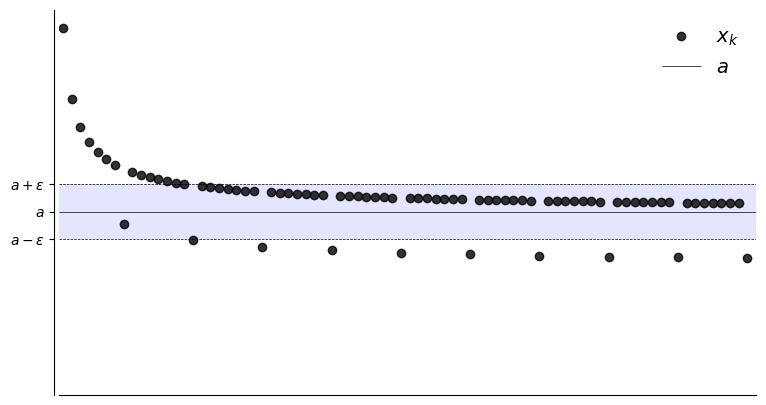
Suppose, for any \(\epsilon > 0\), we can find an \(N \in \mathbb{N}\) such that
alternatively for \(\mathbb{R}\)
Then \(\{x_k\}\) is said to converge to \(a\)
Definition
Sequence \(\{x_k\}\) converges to \(a \in \mathbb{R}\) if
We can say
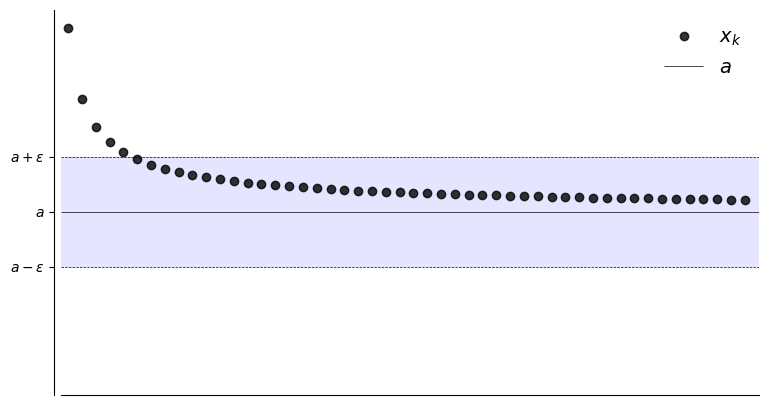
the sequence \(\{x_k\}\) is eventually in the \(\epsilon\)-ball around \(a\)
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
# from matplotlib import rc
# rc('font',**{'family':'serif','serif':['Palatino']})
# rc('text', usetex=True)
def fx(n):
return 1 + 1/(n**(0.7))
def subplots(fs):
"Custom subplots with axes throught the origin"
fig, ax = plt.subplots(figsize=fs)
# Set the axes through the origin
for spine in ['left', 'bottom']:
ax.spines[spine].set_position('zero')
for spine in ['right', 'top']:
ax.spines[spine].set_color('none')
return fig, ax
def plot_seq(N,epsilon,a,fn):
fig, ax = subplots((9, 5))
xmin, xmax = 0.5, N+1
ax.set_xlim(xmin, xmax)
ax.set_ylim(0, 2.1)
n = np.arange(1, N+1)
ax.set_xticks([])
ax.plot(n, fn(n), 'ko', label=r'$x_k$', alpha=0.8)
ax.hlines(a, xmin, xmax, color='k', lw=0.5, label='$a$')
ax.hlines([a - epsilon, a + epsilon], xmin, xmax, color='k', lw=0.5, linestyles='dashed')
ax.fill_between((xmin, xmax), a - epsilon, a + epsilon, facecolor='blue', alpha=0.1)
ax.set_yticks((a - epsilon, a, a + epsilon))
ax.set_yticklabels((r'$a - \epsilon$', r'$a$', r'$a + \epsilon$'))
ax.legend(loc='upper right', frameon=False, fontsize=14)
plt.show()
N = 50
a = 1
plot_seq(N,0.30,a,fx)
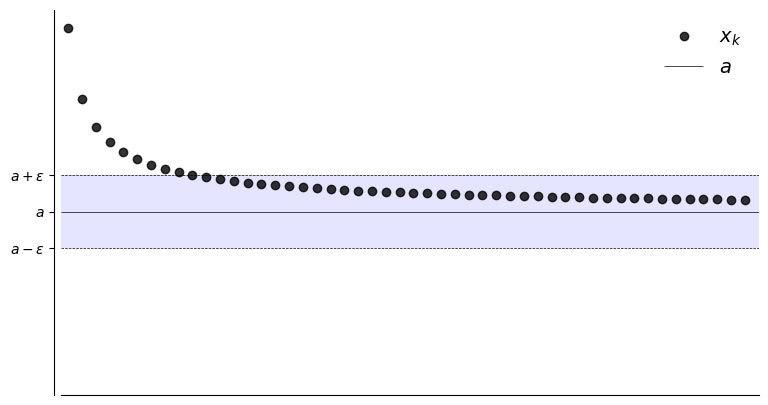
plot_seq(N,0.20,a,fx)
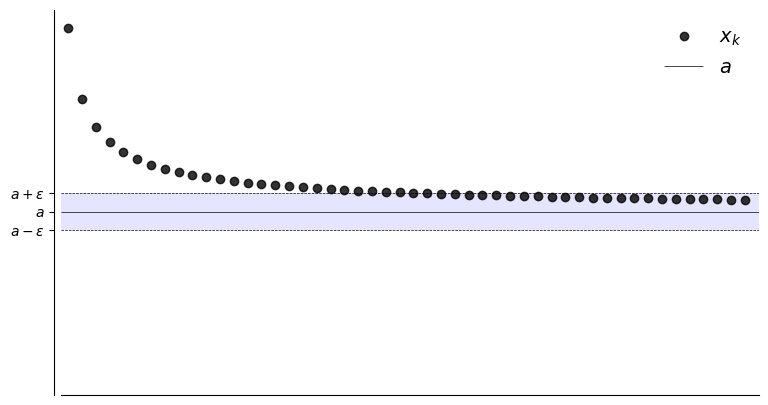
plot_seq(N,0.10,a,fx)
Definition
The point \(a\) is called the limit of the sequence, denoted
if
Example
\(\{x_k\}\) defined by \(x_k = 1 + 1/k\) converges to \(1\):
To prove this we must show that \(\forall \, \epsilon > 0\), there is an \(N \in \mathbb{N}\) such that
To show this formally we need to come up with an “algorithm”
You give me any \(\epsilon > 0\)
I respond with an \(N\) such that equation above holds
In general, as \(\epsilon\) shrinks, \(N\) will have to grow
Proof:
Pick an arbitrary \(\epsilon > 0\)
Now we have to come up with an \(N\) such that
Let \(N\) be the first integer greater than \( 1/\epsilon\)
Then
\(\blacksquare\)
Remark: Any \(N' > N\) would also work
Example
The sequence \(x_k = 2^{-k}\) converges to \(0\) as \(k \to \infty\)
Proof:
Must show that, \(\forall \, \epsilon > 0\), \(\exists \, N \in \mathbb{N}\) such that
So pick any \(\epsilon > 0\), and observe that
Hence we take \(N\) to be the first integer greater than \(- \ln \epsilon / \ln 2\)
Then
What if we want to show that \(x_k \to a\) fails?
To show convergence fails we need to show the negation of
In words, there is an \(\epsilon > 0\) where we can’t find any such \(N\)
That is, for any choice of \(N\) there will be \(n>N\) such that \(x_k\) jumps to the outside \(B_{\epsilon}(a)\)
In other words, there exists a \(B_\epsilon(a)\) such that \(x_k \notin B_\epsilon(a)\) again and again as \(k \to \infty\).
This is the kind of picture we’re thinking of
Show code cell source
def fx2(n):
return 1 + 1/(n**(0.7)) - 0.3 * (n % 8 == 0)
N = 80
a = 1
plot_seq(N,0.15,a,fx2)
Example
The sequence \(x_k = (-1)^k\) does not converge to any \(a \in \mathbb{R}\)
Proof:
This is what we want to show
Since it’s a “there exists”, we need to come up with such an \(\epsilon\)
Let’s try \(\epsilon = 0.5\), so that
We have:
If \(k\) is odd then \(x_k = -1\) when \(k > N\) for any \(N\).
If \(k\) is even then \(x_k = 1\) when \(k > N\) for any \(N\).
Therefore even if \(a=1\) or \(a=-1\), \(\{x_k\}\) not in \(B_\epsilon(a)\) infinitely many times as \(k \to \infty\). It holds for all other values of \(a \in \mathbb{R}\).
\(\blacksquare\)
\(\mathbb{R}^n\)#
Definition
Sequence \(\{x_k\}\) is said to converge to \(a \in \mathbb{R}^n\) if
We can say again that
\(\{x_k\}\) is eventually in any \(\epsilon\)-neighborhood of \(a\)
In this case \(a\) is called the limit of the sequence, and as in one-dimensional case, we write
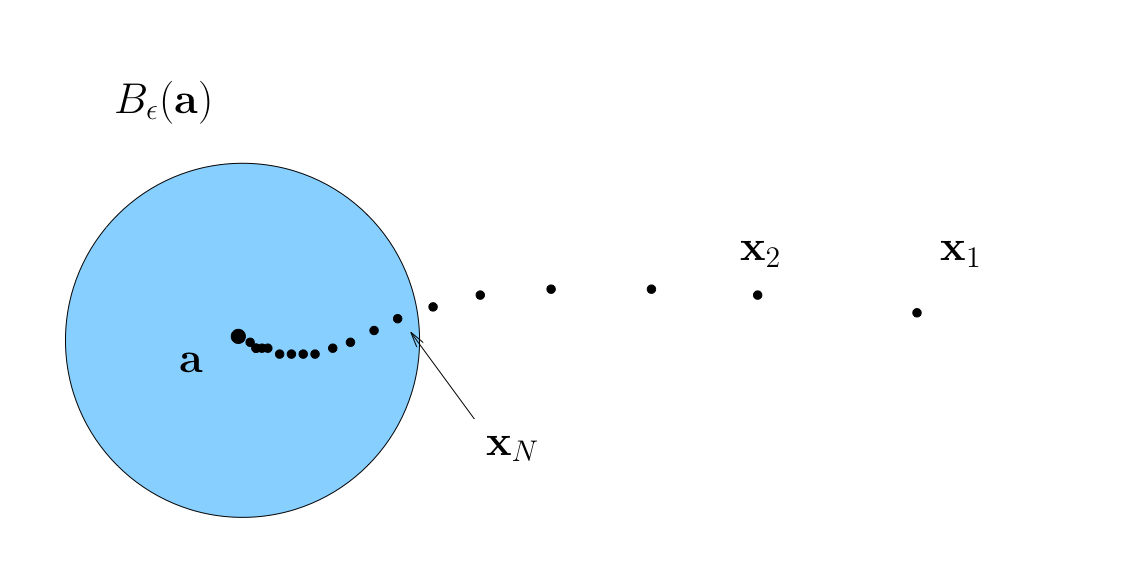
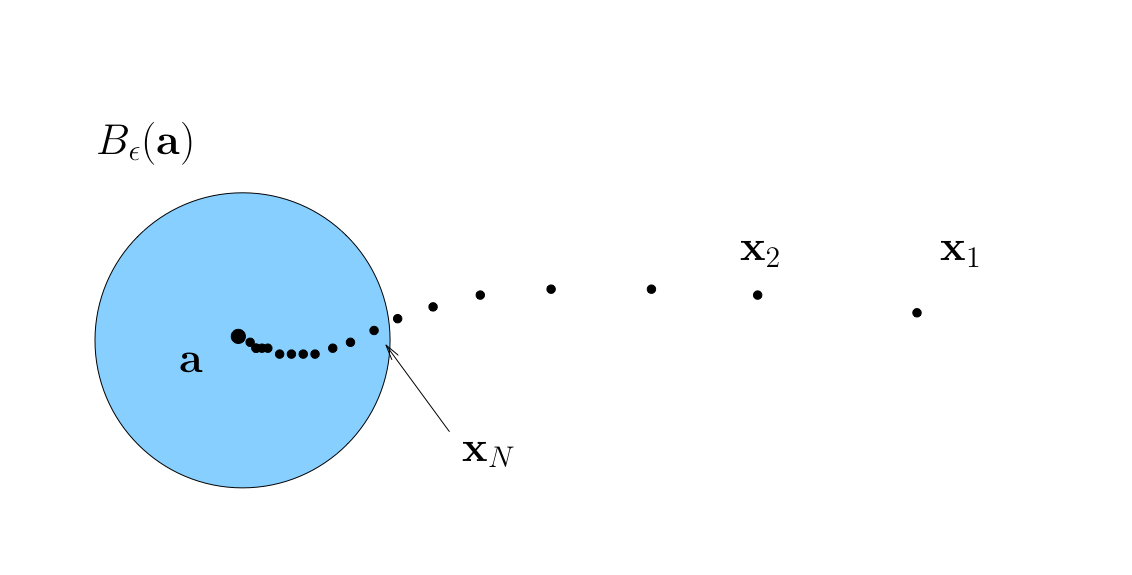
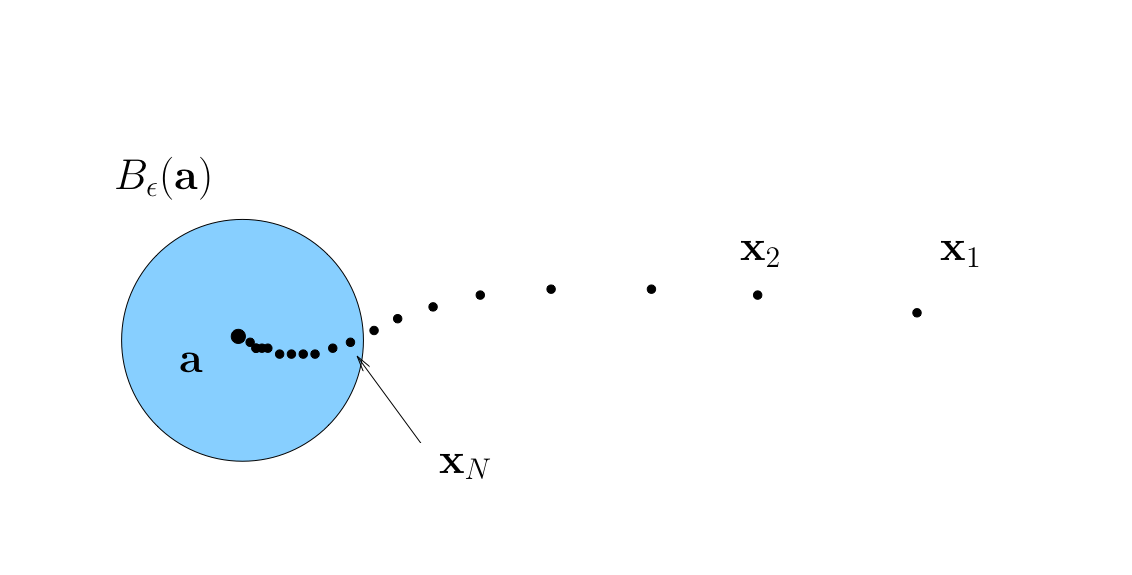
Definition
We call \(\{ x_k \}\) convergent if it converges to some limit in \(\mathbb{R}^n\)
Vector vs Componentwise Convergence#
Fact
A sequence \(\{x_k\}\) in \(\mathbb{R}^n\) converges to \(a \in \mathbb{R}^n\) if and only if each component sequence converges in \(\mathbb{R}\)
That is,
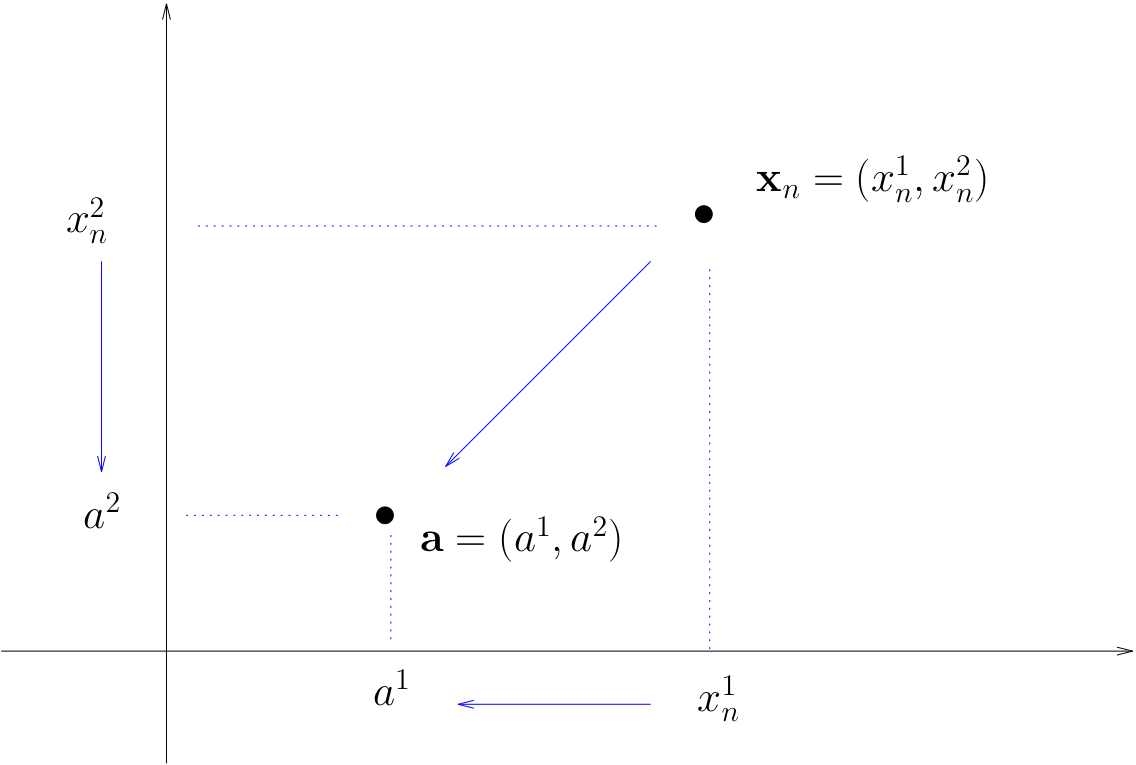
Proof
The sketch of the proof:
\(\Rightarrow\) (necessity): verify that the definition of convergence in \(\mathbb{R}\) corresponds to the convergence in each dimension by definition where \(\epsilon\)-neighborhoods are projection of the \(B_\epsilon(a)\)
\(\Leftarrow\) (sufficiency): verify that convergence in \(\mathbb{R}\) by definition follows from the definitions to the convergence in each dimension when the required \(B_\epsilon(a)\) ball is constructed to contain the hypercube of the \(\epsilon\)-neighborhoods of each dimension.
Properties of limit#
The following facts prove to be very useful in applications and problem sets
Fact
\(x_k \to a\) in \(\mathbb{R}^n\) if and only if \(\|x_k - a\| \to 0\) in \(\mathbb{R}\)
If \(x_k \to x\) and \(y_n \to y\) then \(x_k + y_n \to x + y\)
If \(x_k \to x\) and \(\alpha \in \mathbb{R}\) then \(\alpha x_k \to \alpha x\)
If \(x_k \to x\) and \(y_n \to y\) then \(x_k y_n \to xy\)
If \(x_k \to x\) and \(y_n \to y\) then \(x_k / y_n \to x/y\), provided \(y_n \ne 0\), \(y \ne 0\)
If \(x_k \to x\) then \(x_k^p \to x^p\)
Proof
Let’s prove that
\(x_k \to a\) in \(\mathbb{R}^n\) means that
\(\|x_k - a\| \to 0\) in \(\mathbb{R}\) means that
Obviously equivalent
\(\blacksquare\)
Exercise: Prove other properties using definition of limit
Fact
Each sequence in \(\mathbb{R}^n\) has at most one limit
Proof
Proof for the \(\mathbb{R}\) case.
Suppose instead that \(x_k \to a \text{ and } x_k \to b \text{ with } a \ne b \)
Take disjoint \(\epsilon\)-balls around \(a\) and \(b\)

Since \(x_k \to a\) and \(x_k \to b\),
\(\exists \; N_a\) s.t. \(k \geq N_a \implies x_k \in B_{\epsilon}(a)\)
\(\exists \; N_b\) s.t. \(k \geq N_b \implies x_k \in B_{\epsilon}(b)\)
But then \(n \geq \max\{N_a, N_b\} \implies \) \(x_k \in B_{\epsilon}(a)\) and \(x_k \in B_{\epsilon}(b)\)
Contradiction, as the balls are assumed disjoint
\(\blacksquare\)
Fact
Every convergent sequence is bounded
Proof
This proof is involves bounded sets which are defined in the next lecture 😕
Proof for the \(\mathbb{R}\) case.
Let \(\{x_k\}\) be convergent with \(x_k \to a\)
Fix any \(\epsilon > 0\) and choose \(N\) s.t. \(x_k \in B_{\epsilon}(a)\) when \(k \geq N\)
Regarded as sets,
Both of these sets are bounded
First because finite sets are bounded
Second because \(B_{\epsilon}(a)\) is bounded
Further, finite unions of bounded sets are bounded
\(\blacksquare\)
Cauchy sequences#
Informal definition: Cauchy sequences are those where \(|x_k - x_{k+1}|\) gets smaller and smaller

Example
Sequences generated by iterative methods for solving nonlinear equations often have this property
Show code cell source
f = lambda x: -4*x**3+5*x+1
g = lambda x: -12*x**2+5
def newton(fun,grad,x0,tol=1e-6,maxiter=100,callback=None):
'''Newton method for solving equation f(x)=0
with given tolerance and number of iterations.
Callback function is invoked at each iteration if given.
'''
for i in range(maxiter):
x1 = x0 - fun(x0)/grad(x0)
err = abs(x1-x0)
if callback != None: callback(err=err,x0=x0,x1=x1,iter=i)
if err<tol: break
x0 = x1
else:
raise RuntimeError('Failed to converge in %d iterations'%maxiter)
return (x0+x1)/2
def print_err(iter,err,**kwargs):
x = kwargs['x'] if 'x' in kwargs.keys() else kwargs['x0']
print('{:4d}: x = {:14.8f} diff = {:14.10f}'.format(iter,x,err))
print('Newton method')
res = newton(f,g,x0=123.45,callback=print_err,tol=1e-10)
Newton method
0: x = 123.45000000 diff = 41.1477443465
1: x = 82.30225565 diff = 27.4306976138
2: x = 54.87155804 diff = 18.2854286376
3: x = 36.58612940 diff = 12.1877193931
4: x = 24.39841001 diff = 8.1212701971
5: x = 16.27713981 diff = 5.4083058492
6: x = 10.86883396 diff = 3.5965889909
7: x = 7.27224497 diff = 2.3839931063
8: x = 4.88825187 diff = 1.5680338561
9: x = 3.32021801 diff = 1.0119341175
10: x = 2.30828389 diff = 0.6219125117
11: x = 1.68637138 diff = 0.3347943714
12: x = 1.35157701 diff = 0.1251775194
13: x = 1.22639949 diff = 0.0188751183
14: x = 1.20752437 diff = 0.0004173878
15: x = 1.20710698 diff = 0.0000002022
16: x = 1.20710678 diff = 0.0000000000
Definition
A sequence \(\{x_k\}\) is called Cauchy if
Alternatively
Cauchy sequences allow to establish convergence without finding the limit itself!
Fact
Every convergent sequence is Cauchy, and every Cauchy sequence is convergent.
Proof
Proof of \(\Rightarrow\):
Let \(\{x_k\}\) be a sequence converging to some \(a \in \mathbb{R}\)
Fix \(\epsilon > 0\)
We can choose \(N\) s.t.
For this \(N\) we have \(k \geq N\) and \(j \geq 1\) implies
Proof of \(\Leftarrow\):
Follows from the density property of \(\mathbb{R}\)
\(\blacksquare\)
Example
\(\{x_k\}\) defined by \(x_k = \alpha^k\) where \(\alpha \in (0, 1)\) is Cauchy
Proof:
For any \(k , j\) we have
Fix \(\epsilon > 0\)
We can show that \(k > \log(\epsilon) / \log(\alpha) \implies \alpha^k < \epsilon\)
Hence any integer \(N > \log(\epsilon) / \log(\alpha)\) the sequence is Cauchy by definition.
\(\blacksquare\)
Subsequences#
Definition
A sequence \(\{x_{k_j} \}\) is called a subsequence of \(\{x_k\}\) if
\(\{x_{k_j} \}\) is a subset of \(\{x_k\}\)
\(\{k_j\}\) is sequence of strictly increasing natural numbers
Example
In this case
Example
\(\{\frac{1}{1}, \frac{1}{3}, \frac{1}{5},\ldots\}\) is a subsequence of \(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots\}\)
\(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3},\ldots\}\) is a subsequence of \(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots\}\)
\(\{\frac{1}{2}, \frac{1}{2}, \frac{1}{2},\ldots\}\) is not a subsequence of \(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots\}\)
Fact
If \(\{ x_k \}\) converges to \(x\) in \(\mathbb{R}^n\), then every subsequence of \(\{x_k\}\) also converges to \(x\)
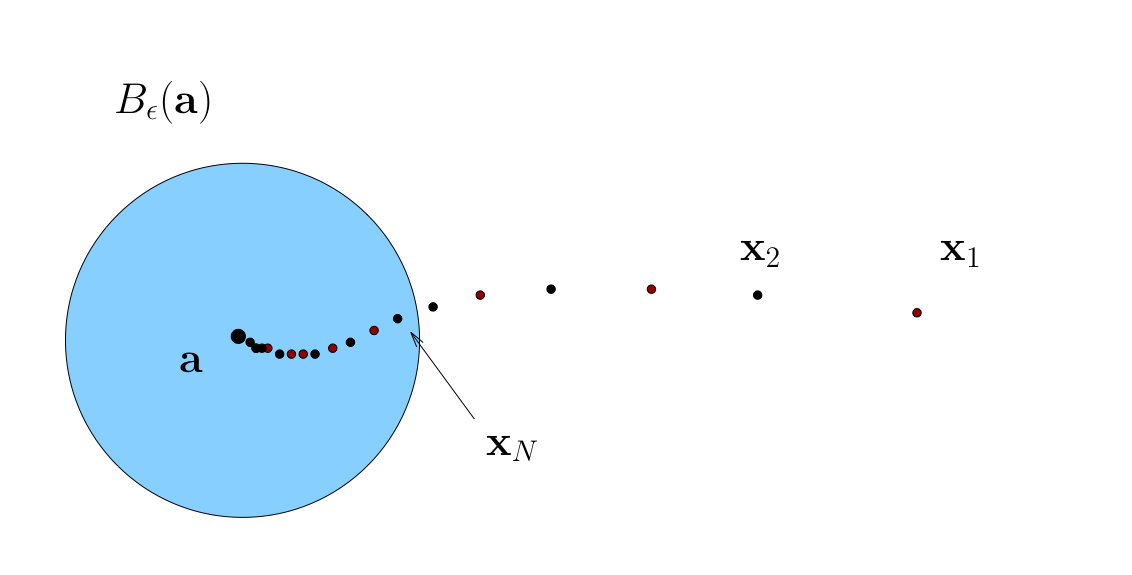
Fig. 15 Convergence of subsequences#
Bolzano-Weierstrass theorem#
This leads us to the famous theorem, which will be part of the proof of the central Weierstrass extreme values theorem, which provides conditions for existence of a maximum and minimum of a function.
Fact: Bolzano-Weierstrass theorem
Every bounded sequence in \(\mathbb{R}^n\) has a convergent subsequence
Proof
Omitted, but see Wiki and resources referenced there.
Limits for functions#
Consider a univariate function \(f: \mathbb{R} \rightarrow \mathbb{R}\) written as \(f(x)\)
The domain of \(f\) is \(\mathbb{R}\), the range of \(f\) is a (possibly improper) subset of \(\mathbb{R}\)
[Spivak, 2006] (p. 90) provides the following informal definition of a limit: “The function \(f\) approaches the limit \(l\) near [the point \(x =\)] \(a\), if we can make \(f(x)\) as close as we like to \(l\) by requiring that \(x\) be sufficiently close to, but unequal to, \(a\).”
Definition
Given the function \(f: A \subset \mathbb{R}^n \to \mathbb{R}\), \(a \in \mathbb{R}\) is a limit of \(f(x)\) as \(x \to x_0 \in A\) if
In this case we write
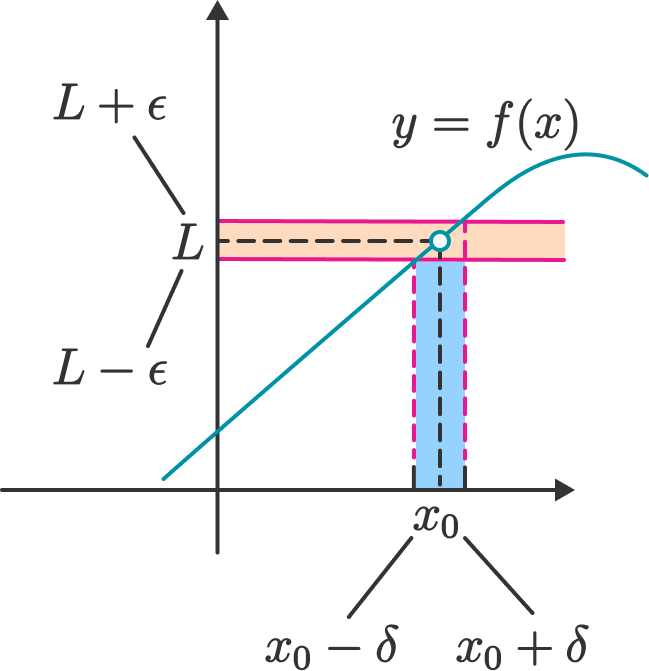
Fig. 16 \(\lim_{x \to x_0} f(x) = L\) under the Cauchy definition#
The absolute value \(|\cdot|\) in this definition plays the role of general distance function \(\|\cdot\|\) which would be appropriate for the functions from \(\mathbb{R}^n\) to \(\mathbb{R}^m\).
Note
Observe that the definition of the limit for functions is very similar to the definition of the limit for sequences, except
\(N \in \mathbb{N}\) is replaced by \(\delta > 0\),
\(k>N\) is replaced by \(\forall x, \, 0 < \|x − x_0\| < \delta\), and
\(|x_k - a| < \epsilon\) is replaced by \(|f(x) - a| < \epsilon\)
note that in the \(\epsilon\)-ball around \(x_0\) the point \(x_0\) is excluded
Heine and Cauchy definitions of the limit for functions#
As a side note, let’s mention that there are two ways to define the limit of a function \(f\).
The definition of the limit for functions above also known as \(\epsilon\)-\(\delta\) definition is due to Augustin-Louis Cauchy.
The alternative definition based on the convergent sequences in the domain of a function is due to Eduard Heine
Definition (Limit of a function due to Heine)
Given the function \(f: A \subset \mathbb{R}^n \to \mathbb{R}\), \(a \in \mathbb{R}\) is a limit of \(f(x)\) as \(x \to x_0 \in A\) if
Fact
Cauchy and Heine definitions of the function limit are equivalent
Therefore we can use the same notation of the definition of the limit of a function
The structure of \(\epsilon–\delta\) arguments#
Suppose that we want to attempt to show that \(\lim _{x \rightarrow a} f(x)=b\).
In order to do this, we need to show that, for any choice \(\epsilon>0\), there exists some \(\delta_{\epsilon}>0\) such that, whenever \(|x-a|<\delta_{\epsilon}\), it is the case that \(|f(x)-b|<\epsilon\).
We write \(\delta_{\epsilon}\) to indicate that the choice of \(\delta\) is allowed to vary with the choice of \(\epsilon\).
An often fruitful approach to the construction of a formal \(\epsilon\)-\(\delta\) limit argument is to proceed as follows:
Start with the end-point that we need to establish: \(|f(x)-b|<\epsilon\).
Use appropriate algebraic rules to rearrange this “final” inequality into something of the form \(|g(x)(x-a)|<\epsilon\).
This new version of the required inequality can be rewritten as \(|g(x)||(x-a)|<\epsilon\).
If \(g(x)=g\), a constant that does not vary with \(x\), then this inequality becomes \(|g||x-a|<\epsilon\). In such cases, we must have \(|x-a|<\frac{\epsilon}{|g|}\), so that an appropriate choice of \(\delta_{\epsilon}\) is \(\delta_{\epsilon}=\frac{\epsilon}{|g|}\).
If \(g(x)\) does vary with \(x\), then we have to work a little bit harder.
Suppose that \(g(x)\) does vary with \(x\). How might we proceed in that case? One possibility is to see if we can find a restriction on the range of values for \(\delta\) that we consider that will allow us to place an upper bound on the value taken by \(|g(x)|\).
In other words, we try and find some restriction on \(\delta\) that will ensure that \(|g(x)|<G\) for some finite \(G>0\). The type of restriction on the values of \(\delta\) that you choose would ideally look something like \(\delta<D\), for some fixed real number \(D>0\). (The reason for this is that it is typically small deviations of \(x\) from a that will cause us problems rather than large deviations of \(x\) from a.)
If \(0<|g(x)|<G\) whenever \(0<\delta<D\), then we have
In such cases, an appropriate choice of \(\delta_{\epsilon}\) is \(\delta_{\epsilon}=\min \left\{\frac{\epsilon}{G}, D\right\}\).
Properties of the limits#
In practice, we would like to be able to find at least some limits without having to resort to the formal “epsilon-delta” arguments that define them. The following rules can sometimes assist us with this.
Fact
Let \(c \in \mathbb{R}\) be a fixed constant, \(a \in \mathbb{R}, \alpha \in \mathbb{R}, \beta \in \mathbb{R}, n \in \mathbb{N}\), \(f: \mathbb{R} \longrightarrow \mathbb{R}\) be a function for which \(\lim _{x \rightarrow a} f(x)=\alpha\), and \(g: \mathbb{R} \longrightarrow \mathbb{R}\) be a function for which \(\lim _{x \rightarrow a} g(x)=\beta\). The following rules apply for limits:
\(\lim _{x \rightarrow a} c=c\) for any \(a \in \mathbb{R}\).
\(\lim _{x \rightarrow a}(c f(x))=c\left(\lim _{x \rightarrow a} f(x)\right)=c \alpha\).
\(\lim _{x \rightarrow a}(f(x)+g(x))=\left(\lim _{x \rightarrow a} f(x)\right)+\left(\lim _{x \rightarrow a} g(x)\right)=\alpha+\beta\).
\(\lim _{x \rightarrow a}(f(x) g(x))=\left(\lim _{x \rightarrow a} f(x)\right)\left(\lim _{x \rightarrow a} g(x)\right)=\alpha \beta\).
\(\lim _{x \rightarrow a}\frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}=\frac{\alpha}{\beta}\) whenever \(\beta \neq 0\).
\(\lim _{x \rightarrow a} \sqrt[n]{f(x)}=\sqrt[n]{\lim _{x \rightarrow a} f(x)}=\sqrt[n]{\alpha}\) whenever \(\sqrt[n]{\alpha}\) is defined.
\(\lim _{x \rightarrow a} \ln f(x)=\ln \lim _{x \rightarrow a} f(x)=\ln \alpha\) whenever \(\ln \alpha\) is defined.
\(\lim _{x \rightarrow a} e^{f(x)}=\exp\big(\lim _{x \rightarrow a} f(x)\big)=e^{\alpha}\)
L’Hopital’s rule: in the indeterminate cases
$\frac{0}{0}$and$\frac{\plusminus\infty}{\plusminus\infty}$\(\lim _{x \rightarrow a}\frac{f(x)}{g(x)}=\lim _{x \rightarrow a}\frac{f'(x)}{g'(x)}\).
Example
This example is drawn from Willis Lauritz Peterson of the University of Utah.
Consider the mapping \(f: \mathbb{R} \longrightarrow \mathbb{R}\) defined by \(f(x)=7 x-4\). We want to show that \(\lim _{x \rightarrow 2} f(x)=10\).
Note that \(|f(x)-10|=|7 x-4-10|=|7 x-14|=|7(x-2)|=\) \(|7||x-2|=7|x-2|\).
We require \(|f(x)-10|<\epsilon\). Note that
Thus, for any \(\epsilon>0\), if \(\delta_{\epsilon}=\frac{\epsilon}{7}\), then \(|f(x)-10|<\epsilon\) whenever \(|x-2|<\delta_{\epsilon}\).
Example
Consider the mapping \(f: \mathbb{R} \longrightarrow \mathbb{R}\) defined by \(f(x)=x^{2}\). We want to show that \(\lim _{x \rightarrow 2} f(x)=4\).
Note that \(|f(x)-4|=\left|x^{2}-4\right|=|(x+2)(x-2)|=|x+2||x-2|\).
Suppose that \(|x-2|<\delta\), which in turn means that \((2-\delta)<x<(2+\delta)\). Thus we have \((4-\delta)<(x+2)<(4+\delta)\).
Let us restrict attention to \(\delta \in(0,1)\). This gives us \(3<(x+2)<5\), so that \(|x+2|<5\).
Thus, when \(|x-2|<\delta\) and \(\delta \in(0,1)\), we have \(|f(x)-4|=|x+2||x-2|<5 \delta\).
We require \(|f(x)-4|<\epsilon\). One way to ensure this is to set \(\delta_{\epsilon}=\min \left(1, \frac{\epsilon}{5}\right)\).
Example
This example is drawn from Willis Lauritz Peterson of the University of Utah.
Consider the mapping \(f: \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x) = x^2 − 3x + 1\).
We want to show that \(lim_{x \rightarrow 2} f(x ) = −1\).
Note that \(|f(x) − (−1)| = |x^2 − 3x + 1 + 1| = |x^2 − 3x + 2| = |(x − 1)(x − 2)| = |x − 1||x − 2|\).
Suppose that \(|x − 2| < \delta\), which in turn means that \((2 − \delta) < x < (2 + \delta)\). Thus we have \((1 − \delta) < (x − 1) < (1 + \delta)\).
Let us restrict attention to \(\delta \in (0, 1)\). This gives us \(0 < (x − 1) < 2\), so that \(|x − 1| < 2\).
Thus, when \(|x − 2| < \delta\) and \(\delta \in (0, 1)\), we have \(|f(x) − (−1)| = |x − 1||x − 2| < 2\delta\).
We require \(|f(x) − (−1)| < \epsilon\). One way to ensure this is to set \(\delta_\epsilon = \min(1, \frac{\epsilon}{2} )\).
Example
Limits can sometimes exist even when the function being considered is not so well behaved. One such example is provided by [Spivak, 2006] (pp. 91–92). It involves the use of a trigonometric function.
The example involves the function \(f: \mathbb{R} \setminus 0 \rightarrow \mathbb{R}\) that is defined by \(f(x) = x sin ( \frac{1}{x})\).
Clearly this function is not defined when \(x = 0\). Furthermore, it can be shown that \(\lim_{x \rightarrow 0} sin ( \frac{1}{x})\) does not exist. However, it can also be shown that \(lim_{x \rightarrow 0} f(x) = 0\).
The reason for this is that \(sin (\theta) \in [−1, 1]\) for all \(\theta \in \mathbb{R}\). Thus \(sin ( \frac{1}{x} )\) is bounded above and below by finite numbers as \(x \rightarrow 0\). This allows the \(x\) component of \(x sin (\frac{1}{x})\) to dominate as \(x \rightarrow 0\).
Example
Limits do not always exist. In this example, we consider a case in which the limit of a function as \(x\) approaches a particular point does not exist.
Consider the mapping \(f: \mathbb{R} \rightarrow \mathbb{R}\) defined by
We want to show that \(\lim_{x \rightarrow 5} f(x)\) does not exist.
Suppose that the limit does exist. Denote the limit by \(l\). Recall that \(d (x, y ) = \{ (y − x )2 \}^{\frac{1}{2}} = |y − x |\). Let \(\delta > 0\).
If \(|5 − x | < \delta\), then \(5 − \delta < x < 5 + \delta\), so that \(x \in (5 − \delta, 5 + \delta)\).
Note that \(x \in (5 − \delta, 5 + \delta) = (5 − \delta, 5) \cup [5, 5 + \delta)\), where \((5 − \delta, 5) \ne \varnothing\) and \([5, 5 + \delta) \ne \varnothing\).
Thus we know the following:
There exist some \(x \in (5 − \delta, 5) \subseteq (5 − \delta, 5 + \delta)\), so that \(f(x) = 0\) for some \(x \in (5 − \delta, 5 + \delta)\).
There exist some \(x \in [5, 5 + \delta) \subseteq (5 − \delta, 5 + \delta)\), so that \(f(x) = 1\) for some \(x \in (5 − \delta, 5 + \delta)\).
The image set under \(f\) for \((5 − \delta, 5 + \delta)\) is \(f ((5 − \delta, 5 + \delta)) = \{ f(x) : x \in (5 − \delta, 5 + \delta) \} = \{ 0, 1 \} \subseteq [0, 1]\).
Note that for any choice of \(\delta > 0\), \([0, 1]\) is the smallest connected interval that contains the image set \(f ((5 − \delta, 5 + \delta)) = \{ 0, 1 \}\).
Hence, in order for the limit to exist, we need \([0, 1] \subseteq (l − \epsilon, l + \epsilon)\) for all \(\epsilon > 0\). But for \(\epsilon \in (0, \frac{1}{2})\), there is no \(l \in \mathbb{R}\) for which this is the case. Thus we can conclude that \(\lim_{x \rightarrow 5} f(x)\) does not exist.
Continuity of functions#
Fundamental property of functions, required not only to establish existence of optima and optimizers, but also roots, fixed points, etc.
Definition
Let \(f \colon A \in \mathbb{R}^n \to \mathbb{R}\)
\(f\) is called continuous at \(x \in A\) if
Note that the definition requires that
\(f(x_k)\) converges for each choice of \(x_k \to x\),
the limit is always the same, and that limit is \(f(x)\)
Definition
\(f: A \to \mathbb{R}\) is called continuous if it is continuous at every \(x \in A\)
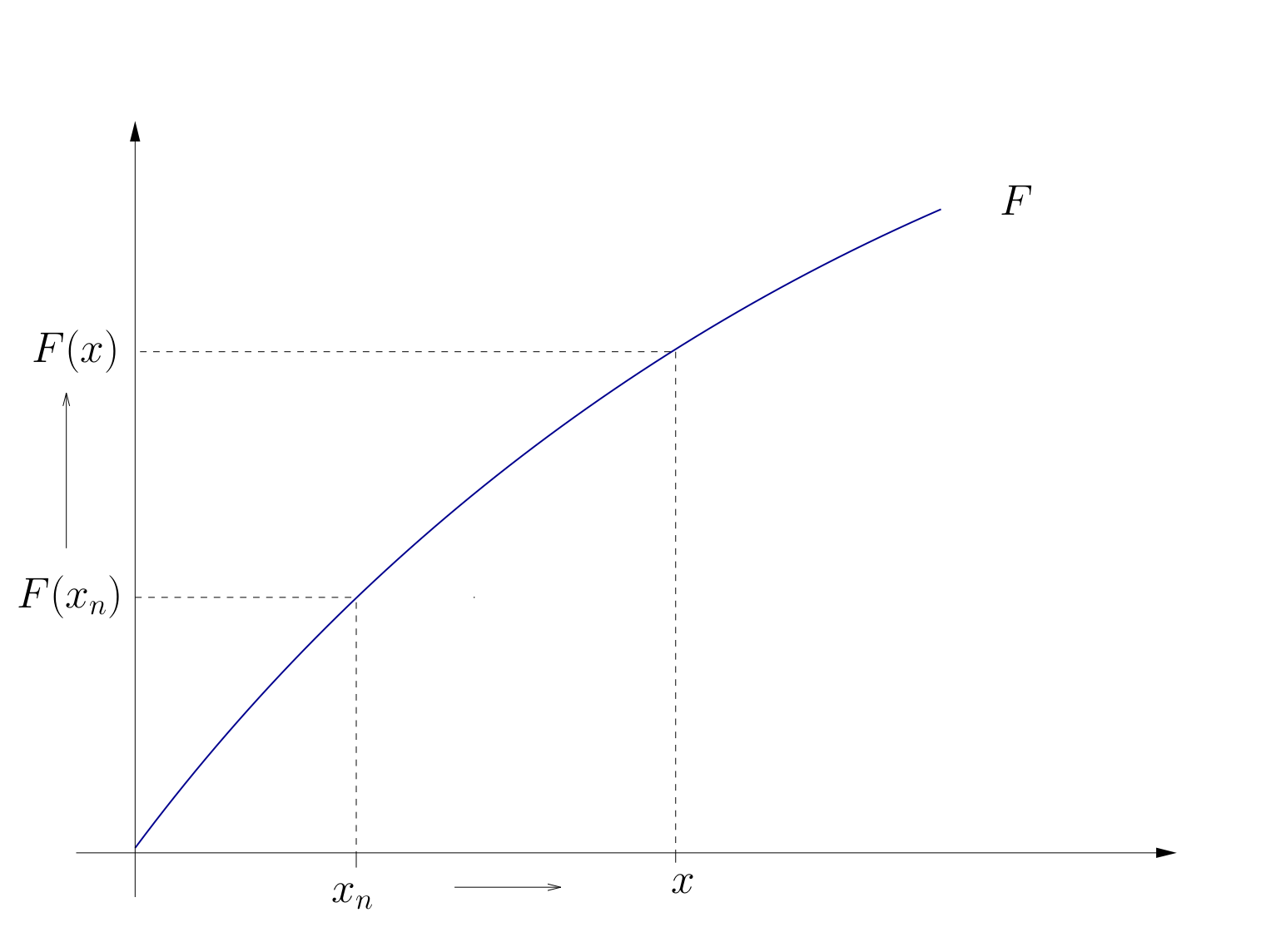
Fig. 17 Continuous function#
Example
Function \(f(x) = \exp(x)\) is continuous at \(x=0\)
Proof:
Consider any sequence \(\{x_k\}\) which converges to \(0\)
We want to show that for any \(\epsilon>0\) there exists \(N\) such that \(k \geq N \implies |f(x_k) - f(0)| < \epsilon\). We have
Because due to \(x_k \to x\) for any \(\epsilon' = \ln(1-\epsilon)\) there exists \(N\) such that \(k \geq N \implies |x_k - 0| < \epsilon'\), we have \(f(x_k) \to f(x)\) by definition. Thus, \(f\) is continuous at \(x=0\).
\(\blacksquare\)
Fact
Some functions known to be continuous on their domains:
\(f: x \mapsto x^\alpha\)
\(f: x \mapsto |x|\)
\(f: x \mapsto \log(x)\)
\(f: x \mapsto \exp(x)\)
\(f: x \mapsto \sin(x)\)
\(f: x \mapsto \cos(x)\)
Types of discontinuities#
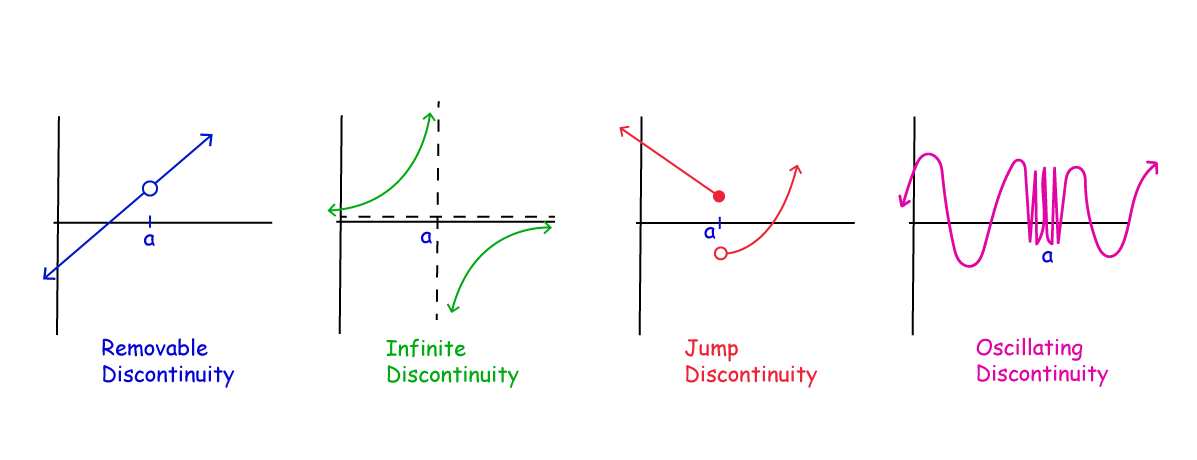
Fig. 18 4 common types of discontinuity#
Example
The indicator function \(x \mapsto \mathbb{1}\{x > 0\}\) has a jump discontinuity at \(0\).
Fact
Let \(f\) and \(g\) be functions and let \(\alpha \in \mathbb{R}\)
If \(f\) and \(g\) are continuous at \(x\) then so is \(f + g\), where
If \(f\) is continuous at \(x\) then so is \(\alpha f\), where
If \(f\) and \(g\) are continuous at \(x\) and real valued then so is \(f \circ g\), where
In the latter case, if in addition \(g(x) \ne 0\), then \(f/g\) is also continuous.
Proof
Just repeatedly apply the properties of the limits
Let’s just check that
Let \(f\) and \(g\) be continuous at \(x\)
Pick any \(x_k \to x\)
We claim that \(f(x_k) + g(x_k) \to f(x) + g(x)\)
By assumption, \(f(x_k) \to f(x)\) and \(g(x_k) \to g(x)\)
From this and the triangle inequality we get
\(\blacksquare\)
As a result, set of continuous functions is “closed” under elementary arithmetic operations
Example
The function \(f \colon \mathbb{R} \to \mathbb{R}\) defined by
is continuous (we just have to be careful to ensure that denominator is not zero – which it is not for all \(x\in\mathbb{R}\))
Example
An example of oscillating discontinuity is the function \(f(x) = \sin(1/x)\) which is discontinuous at \(x=0\).