📖 Determinants, eigenpairs and diagonalization

📖 Determinants, eigenpairs and diagonalization#

⏱ | words

WARNING

This section of the lecture notes is still under construction. It will be ready before the lecture.

Eigenvalues and Eigenvectors#

Let $A$ be a square matrix

Think of $A$ as representing a mapping $x \mapsto A x$, this is a linear function (see prev lecture)

But sometimes $x$ will only be scaled:

\[ % A x = \lambda x \quad \text{for some scalar $\lambda$} % \]

Definition

If $A x = \lambda x$ holds and $x$ is nonzero, then

$x$ is called an eigenvector of $A$ and $\lambda$ is called an eigenvalue
$(x, \lambda)$ is called an eigenpair

Clearly $(x, \lambda)$ is an eigenpair of $A$ $\implies$ $(\alpha x, \lambda)$ is an eigenpair of $A$ for any nonzero $\alpha$

Example

Let

\[\begin{split} % A = \begin{pmatrix} 1 & -1 \\ 3 & 5 \end{pmatrix} % \end{split}\]

Then

\[\begin{split} % \lambda = 2 \quad \text{ and } \quad x = \begin{pmatrix} 1 \\ -1 \end{pmatrix} % \end{split}\]

form an eigenpair because $x \ne 0$ and

\[\begin{split} % A x = \begin{pmatrix} 1 & -1 \\ 3 & 5 \end{pmatrix} \begin{pmatrix} 1 \\ -1 \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \end{pmatrix} = 2 \begin{pmatrix} 1 \\ -1 \end{pmatrix} = \lambda x % \end{split}\]

import numpy as np
A = [[1, 2],
     [2, 1]]
eigvals, eigvecs = np.linalg.eig(A)
for i in range(eigvals.size):
  x = eigvecs[:,i]
  lm = eigvals[i]
  print(f'Eigenpair {i}:\n{lm:.5f} --> {x}')
  print(f'Check Ax=lm*x: {np.dot(A, x)} = {lm * x}')

Eigenpair 0:
3.00000 --> [0.70710678 0.70710678]
Check Ax=lm*x: [2.12132034 2.12132034] = [2.12132034 2.12132034]
Eigenpair 1:
-1.00000 --> [-0.70710678  0.70710678]
Check Ax=lm*x: [ 0.70710678 -0.70710678] = [ 0.70710678 -0.70710678]

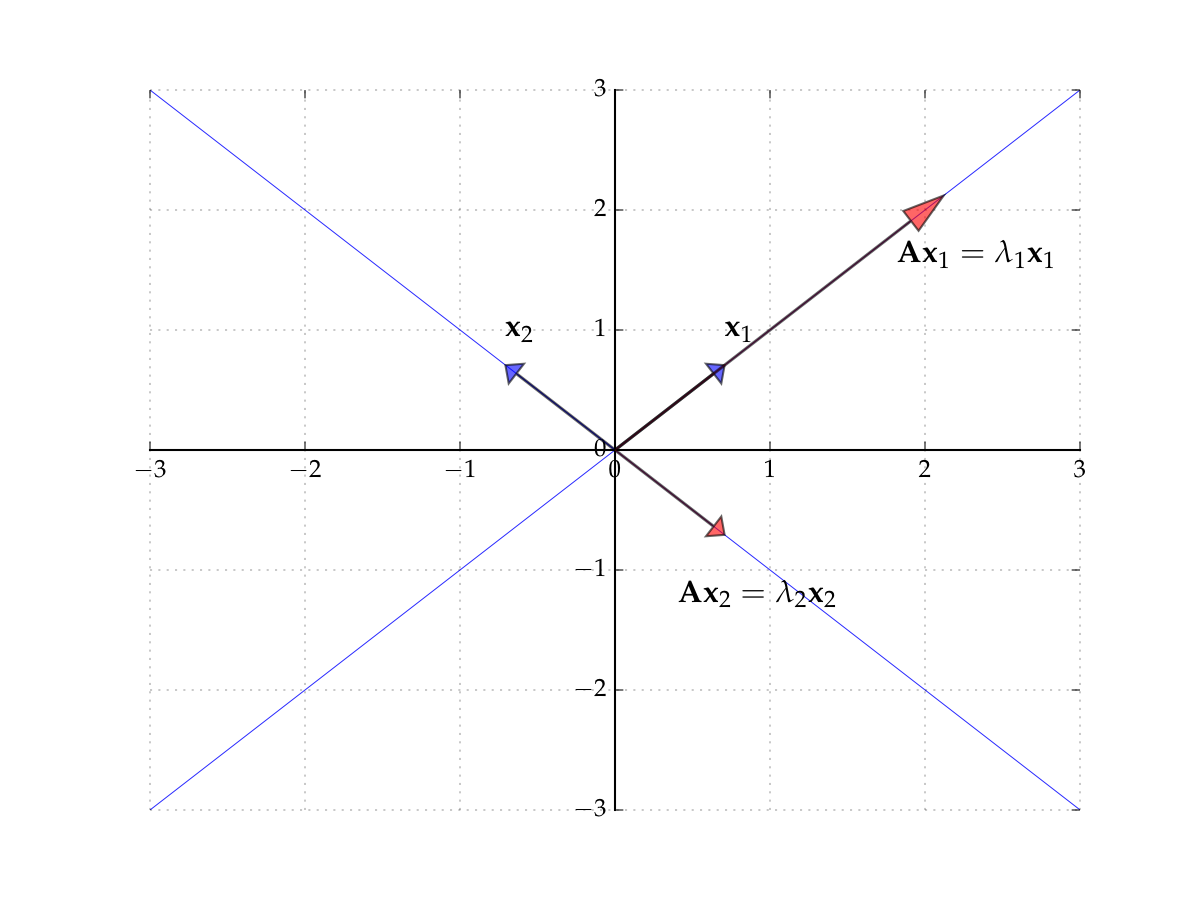
_images/eigenvecs.png — Fig. 42 The eigenvectors of $A$#

Consider the matrix

\[\begin{split} % R = \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \\ \end{array} \right) % \end{split}\]

Induces counter-clockwise rotation on any point by $90^{\circ}$

Hint

The rows of the matrix show where the classic basis vectors are translated to.

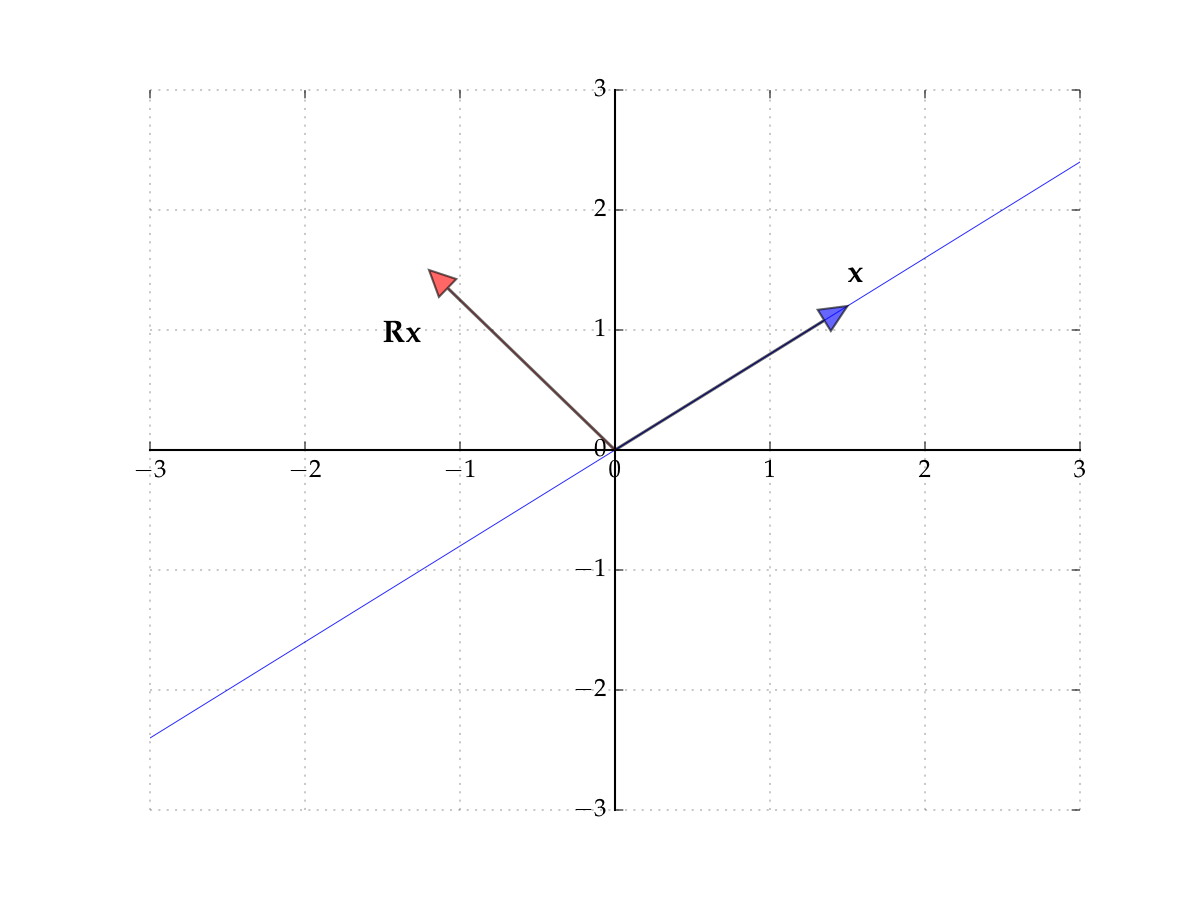
_images/rotation_1.png — Fig. 43 The matrix $R$ rotates points by $90^{\circ}$#

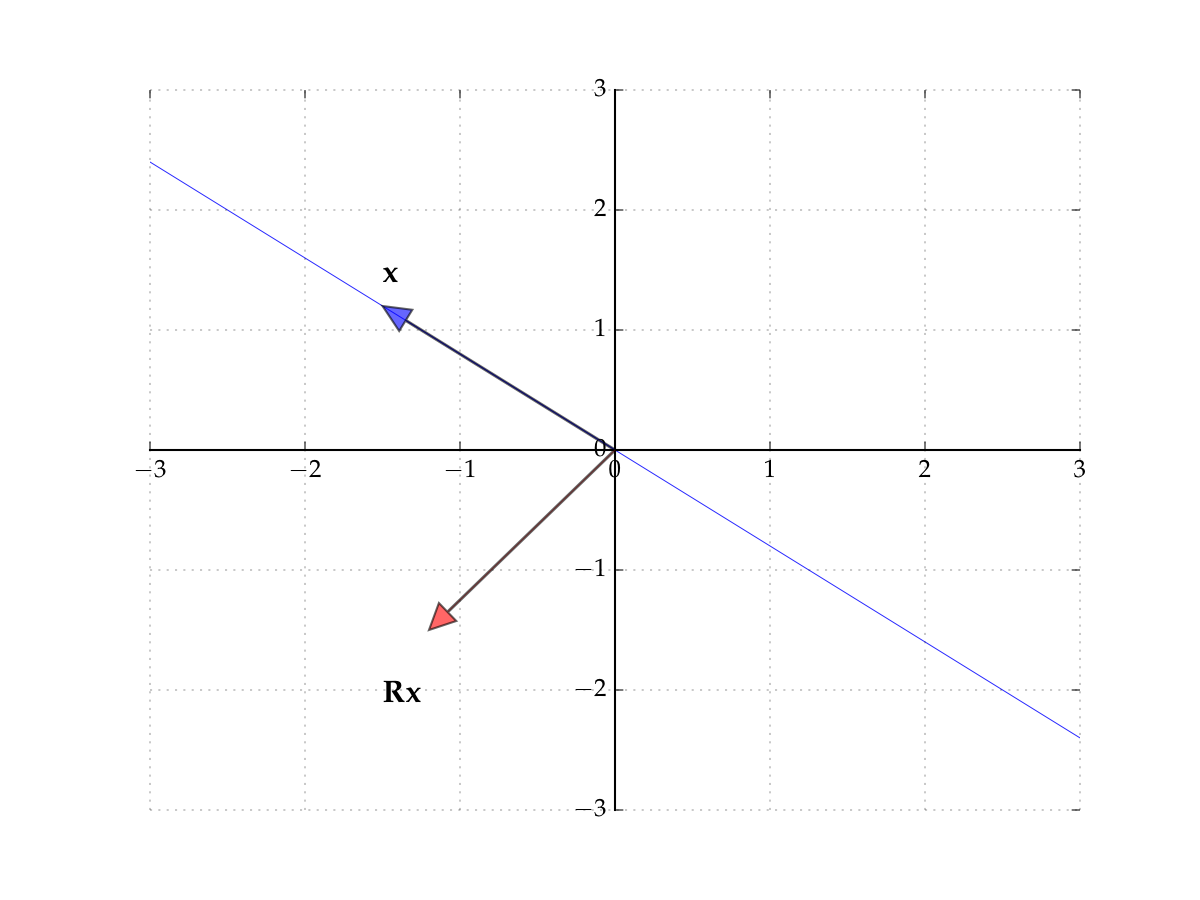
_images/rotation_2.png — Fig. 44 The matrix $R$ rotates points by $90^{\circ}$#

Hence no point $x$ is scaled

Hence there exists no pair $\lambda \in \mathbb{R}$ and $x \ne 0$ such that

\[R x = \lambda x\]

In other words, no real-valued eigenpairs exist. However, if we allow for complex values, then we can find eigenpairs even for this case

Eigenvalues and determinants#

Fact

For any square matrix $A$

\[ % \lambda \text{ is an eigenvalue of } A \; \iff \; \det(A - \lambda I) = 0 % \]

Proof

Let $A$ by $N \times N$ and let $I$ be the $N \times N$ identity

We have

\[\begin{split} % \det(A - \lambda I) = 0 \iff A - \lambda I \text{ is singular} \\ \iff \exists \, x \ne 0 \text{ such that } (A - \lambda I) x = 0 \\ \iff \exists \, x \ne 0 \text{ such that } A x = \lambda x \\ \iff \lambda \text{ is an eigenvalue of } A % \end{split}\]

Example

In the $2 \times 2$ case,

\[\begin{split} % A = \left( \begin{array}{cc} a & b \\ c & d \\ \end{array} \right) \quad \implies \quad A - \lambda I = \left( \begin{array}{cc} a - \lambda & b \\ c & d - \lambda \end{array} \right) % \end{split}\]

\[\begin{split} % \implies \det(A - \lambda I) = (a - \lambda)(d - \lambda) - bc \\ = \lambda^2 - (a + d) \lambda + (ad - bc) % \end{split}\]

Hence the eigenvalues of $A$ are given by the two roots of

\[ % \lambda^2 - (a + d) \lambda + (ad - bc) = 0 % \]

Equivalently,

\[ % \lambda^2 - \mathrm{trace}(A) \lambda + \det(A) = 0 % \]

Existence of Eigenvalues#

For an $(N \times N)$ matrix $A$ expression $\det(A - \lambda I) = 0$ is a polynomial equation of degree $N$ in $\lambda$

to see this, imagine how $\lambda$ enters into the computation of the determinant using the definition along the first row, then first row of the first minor submatrix, and so on
the highest degree of $\lambda$ is then the same as the dimension of $A$

Definition

The polynomial $\det(A - \lambda I)$ is called a characteristic polynomial of $A$.

The roots of the characteristic equation $\det(A - \lambda I) = 0$ determine all eigenvalues of $A$.

By the Fundamental theorem of algebra there are $N$ of such (complex) roots $\lambda_1, \ldots, \lambda_N$, and we can write

\[ % \det(A - \lambda I) = \prod_{n=1}^N (\lambda_n - \lambda) % \]

Each such $\lambda_i$ is an eigenvalue of $A$ because

\[ % \det(A - \lambda_i I) = \prod_{n=1}^N (\lambda_n - \lambda_i) = 0 % \]

Note: not all roots are necessarily distinct — there can be repeats

Diagonalization#

Consider a square $N \times N$ matrix $A$

\[\begin{split} % A = \left( \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1N} \\ a_{21} & a_{22} & \cdots & a_{2N} \\ \vdots & \vdots & & \vdots \\ a_{N1} & a_{N2} & \cdots & a_{NN} \\ \end{array} \right) % \end{split}\]

Definition

The $N$ elements of the form $a_{nn}$ are called the principal diagonal

Definition

A square matrix $D$ is called diagonal if all entries off the principal diagonal are zero

\[\begin{split} % D = \left( \begin{array}{cccc} d_1 & 0 & \cdots & 0 \\ 0 & d_2 & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & d_N \\ \end{array} \right) % \end{split}\]

Often written as

\[ % D = \mathrm{diag}(d_1, \ldots, d_N) % \]

Diagonal matrixes are very nice to work with!

Example

\[\begin{split} [\mathrm{diag}(d_1, \ldots, d_N) ]^2 = \left( \begin{array}{cccc} d_1 & 0 & \cdots & 0 \\ 0 & d_2 & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & d_N \\ \end{array} \right)^2 = \left( \begin{array}{cccc} d_1^2 & 0 & \cdots & 0 \\ 0 & d_2^2 & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & d_N^2 \\ \end{array} \right) = \mathrm{diag}(d_1^2, \ldots, d_N^2) \end{split}\]

Fact

If $D = \mathrm{diag}(d_1, \ldots,d_N)$ then

$D^k = \mathrm{diag}(d^k_1, \ldots, d^k_N)$ for any $k \in \mathbb{N}$
$d_n \geq 0$ for all $n$ $\implies$ $D^{1/2}$ exists and equals

\[\mathrm{diag}(\sqrt{d_1}, \ldots, \sqrt{d_N})\]

$d_n \ne 0$ for all $n$ $\implies$ $D$ is nonsingular and

\[D^{-1} = \mathrm{diag}(d_1^{-1}, \ldots, d_N^{-1})\]

Example

Let’s find eigenvalues and eigenvectors of $D = \mathrm{diag}(d_1, \ldots,d_N)$.

The characteristic polynomial is given by

\[\begin{split} \det(D-\lambda I) = \left| \begin{array}{cccc} d_1 - \lambda & 0 & \cdots & 0 \\ 0 & d_2 - \lambda & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & d_N - \lambda \\ \end{array} \right| = \Pi_{i=1}^N (d_i - \lambda) \end{split}\]

Therefore the diagonal elements are the eigenvalues of $D$!

Change of basis#

Consider a vector $x\in \mathbb{R}^N$ which has coordinates $(x_1,x_2,\dots,x_N)$ in classis basis $(e_1,e_2,\dots,e_N)$, where $e_i = (0,\dots,0,1,0\dots,0)^T$

Coordinates of a vector is what we call the coefficients of the linear combination of the basis vectors that gives the vector

We have

\[ x = \sum_{i=1}^N x_i e_i \]

Consider a different basis in $\mathbb{R}^N$ (recall the definition) denoted $(e'_1,e'_2,\dots,e'_N)$ Here we assume that each $e'_i$ is written in the coordinates corresponding to the original basis $(e_1,e_2,\dots,e_N)$.

The coordinates of vector $x$ in basis $(e'_1,e'_2,\dots,e'_N)$ denoted $x' = (x'_1,x'_2,\dots,x'_N)$ are by definition

\[\begin{split} x = \sum_{i=1}^N x'_i e'_i = x'_1 \left( \begin{array}{c} \vdots \\ e'_1 \\ \vdots \end{array} \right) + \dots + x'_N \left( \begin{array}{c} \vdots \\ e'_N \\ \vdots \end{array} \right) = P x' \end{split}\]

Definition

The transformation matrix from the basis $(e_1,e_2,\dots,e_N)$ to $(e'_1,e'_2,\dots,e'_N)$ is given by

\[\begin{split} P = \left( \begin{array}{cccc} \vdots & \vdots & & \vdots \\ e'_1, & e'_2, & \dots & e'_N \\ \vdots & \vdots & & \vdots \end{array} \right) \end{split}\]

In other words, the same vector has coordinates $x = (x_1,x_2,\dots, x_N)$ in the original basis $(e_1,e_2,\dots,e_N)$ and $x' = (x'_1,x'_2,\dots, x'_N)$ in the new basis $(e'_1,e'_2,\dots,e'_N)$, and it holds

\[ x = P x', \quad x' = P^{-1} x \]

We now have a way to represent the same vector in different bases, i.e. change basis!

Example

\[\begin{split} \begin{array}{l} e'_1 = e_1 + e_2 \\ e'_2 = e_1 - e_2 \\ e'_3=e_3 \end{array} \implies P = \begin{pmatrix} 1 & 1 & 0 \\ 1 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{split}\]

Fact

The transformation matrix $P$ is nonsingular (invertible).

Proof

Because the transformation matrix maps a set of basis vectors to another set of basis vectors, they are linearly independent. By the properties of linear functions, $P$ is then non-singular, and $P^{-1}$ exists. $\blacksquare$

Linear functions in different bases#

Consider a linear map $A: x \mapsto Ax$ where $x \in \mathbb{R}^N$

Can we express the same linear map in a different basis?

Let $B$ be the matrix representing the same linear map in a new basis, where the transformation matrix is given by $P$.

\[ x \mapsto Ax \quad \iff \quad x' \mapsto Bx' \]

If the linear map is the same, we must have

\[ Ax = P B P^{-1}x \]

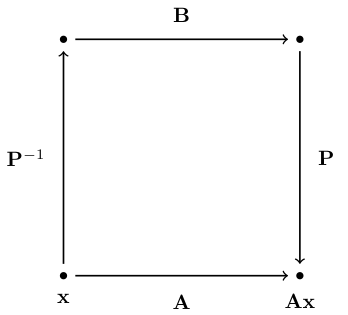
Definition

Square matrix $A$ is said to be similar to square matrix $B$ if there exist an invertible matrix $P$ such that $A = P B P^{-1}$.

Similar matrixes also happen to be very useful!

Example

Consider $A$ that is similar to a diagonal matrix $D = \mathrm{diag}(d_1,\dots,d_N)$.

To find the $A^n$ we can use the fact that

\[ A^2 = AA = P D P^{-1} P D P^{-1} = P D^2 P^{-1} \]

and therefore it’s easy to show by mathematical induction that

\[ A^k = AA = P D P^{-1} P D P^{-1} = A^k = \]

Given the properties of the diagonal matrixes, we have an easily computed expression

\[ A^k = P [\mathrm{diag}(d_1^k,\dots,d_N^k)] P^{-1} \]

Diagonalization using eigenvectors#

Definition

If $A$ is similar to a diagonal matrix, then $A$ is called diagonalizable

Fact (Diagonalizable $\longrightarrow$ Eigenpairs)

Let $A$ be diagonalizable with $A = P D P^{-1}$ and let

$D = \mathrm{diag}(\lambda_1, \ldots, \lambda_N)$
$p_n$ for $n=1,\dots,N$ be the columns of $P$

Then $(p_n, \lambda_n)$ is an eigenpair of $A$ for each $n$

Proof

From $A = P D P^{-1}$ we get $A P = P D$

Equating $n$-th column on each side gives

\[ % A p_n = \lambda_n p_n % \]

Moreover $p_n \ne 0$ because $P$ is invertible (which facts?)

Fact (Distinct eigenvalues $\longrightarrow$ diagonalizable)

If $N \times N$ matrix $A$ has $N$ distinct eigenvalues $\lambda_1, \ldots, \lambda_N$, then $A$ is diagonalizable as $A = P D P^{-1}$ where

$D = \mathrm{diag}(\lambda_1, \ldots, \lambda_N)$
each $n$-th column of $P$ is equal to the eigenvector for $\lambda_n$

Example

Let

\[\begin{split} % A = \begin{pmatrix} 1 & -1 \\ 3 & 5 \end{pmatrix} % \end{split}\]

The eigenvalues of $A$ are 2 and 4, while the eigenvectors are

\[\begin{split} % p_1 = \begin{pmatrix} 1 \\ -1 \end{pmatrix} \quad \text{and} \quad p_2 = \begin{pmatrix} 1 \\ -3 \end{pmatrix} % \end{split}\]

Hence

\[ % A = P \mathrm{diag}(2, 4) P^{-1} % \]

import numpy as np
from numpy.linalg import inv
A = np.array([[1, -1],
              [3, 5]])
eigvals, eigvecs = np.linalg.eig(A)
D = np.diag(eigvals)
P = eigvecs
print('A =',A,sep='\n')
print('D =',D,sep='\n')
print('P =',P,sep='\n')
print('P^-1 =',inv(P),sep='\n')
print('P*D*P^-1 =',P@D@inv(P),sep='\n')

A =
[[ 1 -1]
 [ 3  5]]
D =
[[2. 0.]
 [0. 4.]]
P =
[[-0.70710678  0.31622777]
 [ 0.70710678 -0.9486833 ]]
P^-1 =
[[-2.12132034 -0.70710678]
 [-1.58113883 -1.58113883]]
P*D*P^-1 =
[[ 1. -1.]
 [ 3.  5.]]

Profit!#

Fact

Given $N \times N$ matrix $A$ with distinct eigenvalues $\lambda_1, \ldots, \lambda_N$ we have

If $A = \mathrm{diag}(d_1, \ldots, d_N)$, then $\lambda_n = d_n$ for all $n$
$\det(A) = \prod_{n=1}^N \lambda_n$
If $A$ is symmetric, then $\lambda_n \in \mathbb{R}$ for all $n$ (not complex!)

Proof

The first statement can be checked directly by verifying that the classic basis vectors are eigenvectors of $A$.

The second statement follows from the properties of the determinant of a product:

\[\begin{split} \det(A) = \det(P \mathrm{diag}(\lambda_1,\dots,\lambda_N) P^{-1}) =\\= \det(P) \det(\mathrm{diag}(\lambda_1,\dots,\lambda_N)) \det(P^{-1}) =\\= det(P) \prod_{n=1}^N \lambda_n (\det(P))^{-1} = \prod_{n=1}^N \lambda_n \end{split}\]

The third statement requires complex analysis, we take for granted.

Fact

$A$ is nonsingular $\iff$ all eigenvalues are nonzero

Proof

$A$ is nonsingular $\iff$ $\det(A) \ne 0$ $\iff$ $\prod_{n=1}^N \lambda_n \ne 0$ $\iff$ all $\lambda_n \ne 0$

Fact

If $A$ is nonsingular, then eigenvalues of $A^{-1}$ are $1/\lambda_1, \ldots, 1/\lambda_N$

Proof

\[ A x = \lambda x \iff A^{-1}A x = \lambda A^{-1} x \iff x/\lambda = A^{-1} x \]

Diagonalization of symmetric matrices#

📖 Determinants, eigenpairs and diagonalization

Contents

📖 Determinants, eigenpairs and diagonalization#

Eigenvalues and Eigenvectors#

Eigenvalues and determinants#

Existence of Eigenvalues#

Diagonalization#

Change of basis#

Linear functions in different bases#

Diagonalization using eigenvectors#

Profit!#

Diagonalization of symmetric matrices#

References and reading#