📖 Fundamentals of optimization

📖 Fundamentals of optimization#

⏱ | words

The goal is Weierstrass extreme value theorem which establishes the existence of max and min for continuous functions over compact sets

Talk about sets in \(\mathbb{R}\) first \(\rightarrow\) then transitions to functions

In the introductory lecture we have seen a few simple examples of optimization problems:

  • a solution exists

  • the solution is unique and not hard to find

However, for the majority of problems such properties aren’t guaranteed

We need some idea of how to check whether a solution to an optimization problems even exists!

Consider the problem of finding the “maximum” or “minimum” of a function

A first issue is that such values might not be well defined

Recall that the set of maximizers/minimizers can be

  • empty

  • a singleton (contains one element)

  • infinite (contains infinitely many elements)

Hide code cell content 
from myst_nb import glue
import matplotlib.pyplot as plt
import numpy as np

def subplots():
    "Custom subplots with axes through the origin"
    fig, ax = plt.subplots()
    # Set the axes through the origin
    for spine in ['left', 'bottom']:
        ax.spines[spine].set_position('zero')
    for spine in ['right', 'top']:
        ax.spines[spine].set_color('none')
    return fig, ax

xmin, xmax = 0, 1
xgrid1 = np.linspace(xmin, xmax, 100)
xgrid2 = np.linspace(xmax, 2, 10)

fig, ax = subplots()
ax.set_ylim(0, 1.1)
ax.set_xlim(-0.0, 2)
func_string = r'$f(x) = x^2$ if $x < 1$ else $f(x) = 0.5$'
ax.plot(xgrid1, xgrid1**2, 'b-', lw=3, label=func_string)
ax.plot(xgrid2, -0.25 * xgrid2 + 0.5, 'b-', lw=3)
ax.plot(xgrid1[-1], xgrid1[-1]**2, marker='o', markerfacecolor='white', markeredgewidth=2, markersize=6, color='b')
ax.plot(xgrid2[0], -0.25 * xgrid2[0] + 0.5, marker='.', markerfacecolor='b', markeredgewidth=2, markersize=10, color='b')
glue("fig_none", fig, display=False)

Example: no maximizers

The following function has no maximizers on \([0, 2]\)

\[\begin{split} f(x) = \begin{cases} x^2 & \text{ if } x < 1 \\ 1/2 & \text{ otherwise} \end{cases} \end{split}\]
_images/c2991d08c4e885f6ee5c4699c41bab48dcbf75856d6c05503b71a40b8afd5b7a.png

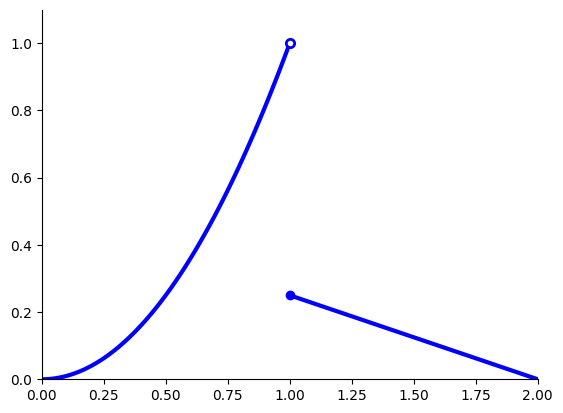
Fig. 39 No maximizer on \([0, 2]\)#

Suprema and Infima (\(\mathrm{sup}\) + \(\mathrm{inf}\))#

  • Always well defined

  • Agree with max and min when the latter exist

Definition

Let \(A \subset \mathbb{R}\) (we restrict attention to subsets of real line for now)

A number \(u \in \mathbb{R}\) is called an upper bound of \(A\) if

\[a \leqslant u \quad \text{for all} \quad a \in A\]

Example

If \(A = (0, 1)\) then 10 is an upper bound of \(A\) — indeed, every element of \((0, 1)\) is \(\leqslant 10\)

If \(A = (0, 1)\) then 1 is an upper bound of \(A\) — indeed, every element of \((0, 1)\) is \(\leqslant 1\)

If \(A = (0, 1)\) then \(0.75\) is not an upper bound of \(A\)

Definition

Let \(U(A)\) denote set of all upper bounds of \(A\).

A set \(A \subset \mathbb{R}\) is called bounded above if \(U(A)\) is not empty

Examples

  • If \(A = [0, 1]\), then \(U(A) = [1, \infty)\)

  • If \(A = (0, 1)\), then \(U(A) = [1, \infty)\)

  • If \(A = (0, 1) \cup (2, 3)\), then \(U(A) = [3, \infty)\)

  • If \(A = \mathbb{N}\), then \(U(A) = \varnothing\)

Definition

The least upper bound \(s\) of \(A\) is called supremum of \(A\), denoted \(s=\sup A\), i.e.

\[s \in U(A) \quad \text{and} \quad s \leqslant u, \; \forall \, u \in U(A)\]

Example

If \(A = (0, 1]\), then \(U(A) = [1, \infty)\), so \(\sup A = 1\)

If \(A = (0, 1)\), then \(U(A) = [1, \infty)\), so \(\sup A = 1\)

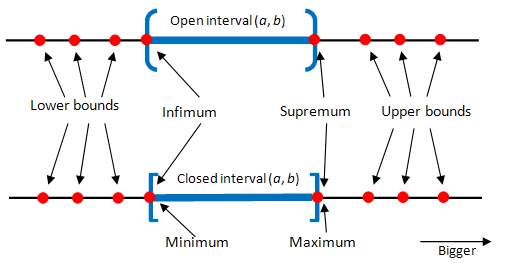
_images/sup_inf_set.png

Fig. 40 Upper and lower bounds, supremum and infimum of an interval on \(\mathbb{R}\)#

Definition

A lower bound of \(A \subset \mathbb{R}\) is any \(\ell \in \mathbb{R}\) such that \(\ell \leqslant a\) for all \(a \in A\).

Let \(L(A)\) denote set of all lower bounds of \(A\).

A set \(A \subset \mathbb{R}\) is called bounded below if \(L(A)\) is not empty.

The highest of the lower bounds \(p\) is called the infimum of \(A\), denoted \(p=\inf A\), i.e.

\[p \in L(A) \quad \text{and} \quad p \geqslant \ell, \; \forall \, \ell \in L(A)\]

Example

  • If \(A = [0, 1]\), then \(\inf A = 0\)

  • If \(A = (0, 1)\), then \(\inf A = 0\)

Some useful facts#

Fact

Boundedness of a subset of the set of real numbers is equivalent to it being bounded above and below.

\[A \subset \mathbb{R}, \; \text{bounded} \quad \iff \quad A \; \text{bounded above and below}\]

Proof

The proof follows trivially from the definitions

Fact

Every nonempty subset of \(\mathbb{R}\) bounded above has a supremum in \(\mathbb{R}\)

Every nonempty subset of \(\mathbb{R}\) bounded below has an infimum in \(\mathbb{R}\)

Proof

Similar to the proof that all Cauchy sequences converge, follows from the density property of \(\mathbb{R}\)

Some textbooks allow all sets to have a supremum and infimum, even if they are not bounded. This is achieved by extending the set of real numbers with \(\{-\infty,\infty\}\)

Then, if \(A\) is unbounded above then \(\sup A = \infty\), and if \(A\) is unbounded below then \(\inf A = -\infty\).

Note

Aside: Conventions for dealing with symbols “\(\infty\)’’ and “\(-\infty\)” If \(a \in \mathbb{R}\), then

  • \(a + \infty = \infty\)

  • \(a - \infty = -\infty\)

  • \(a \times \infty = \infty\) if \(a \ne 0\), \(0 \times \infty = 0\)

  • \(-\infty < a < \infty\)

  • \(\infty + \infty = \infty\)

  • \(-\infty - \infty = -\infty\) But \(\infty - \infty\) is not defined

Fact

Let \(A\) be any set bounded above and let \(s = \sup A\). There exists a sequence \(\{x_n\}\) in \(A\) with \(x_n \to s\).

Analogously, if \(A\) is bounded below and \(p = \inf A\), then there exists a sequence \(\{x_n\}\) in \(A\) with \(x_n \to p\).

Proof

Note that

\[ % \forall \, n \in \mathbb{N}, \;\; \exists \, x_n \in A \; \text{ such that } \; x_n > s - \frac{1}{n} % \]
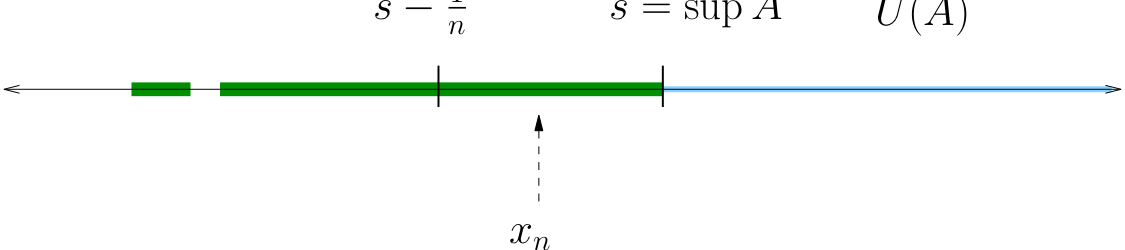
_images/sup_seq.png

(Otherwise \(s\) is not a sup, because \(s-\frac{1}{n}\) is a smaller upper bound)

The sequence \(\{x_n\}\) lies in \(A\) and converges to \(s\).

The proof for the infimum is analogous.

Maxima and Minima (\(\max\) + \(\min\))#

Definition

We call \(a^*\) the maximum of \(A \subset \mathbb{R}\), denoted \(a^* = \max A\), if

\[a^* \in A \quad \text{and} \quad a \leqslant a^* \text{ for all } a \in A \]

We call \(a^*\) the minimum of \(A \subset \mathbb{R}\) and write \(a^* = \min A\) if

\[a^* \in A \quad \text{and} \quad a^* \leqslant a \text{ for all } a \in A \]

Example

For \(A = [0, 1]\) \(\max A = 1\) and \(\min A = 0\)

Relationship between max/min and sup/inf#

Fact

Let \(A\) be any subset of \(\mathbb{R}\)

  1. If \(\sup A \in A\), then \(\max A\) exists and \(\max A = \sup A\)

  2. If \(\inf A \in A\), then \(\min A\) exists and \(\min A = \inf A\)

In other words, when max and min exist they agree with sup and inf

Proof

Proof of case 1: Let \(a^* = \sup A\) and suppose \(a^* \in A\)

We want to show that \(\max A = a^*\)

Since \(a^* \in A\), we need only show that \(a \leqslant a^*\) for all \(a \in A\)

This follows from \(a^* = \sup A\), which implies \(a^* \in U(A)\)

Fact

If \(F \subset \mathbb{R}\) is a closed and bounded, then \(\max F\) and \(\min F\) both exist

Proof

Proof for the max case:

Since \(F\) is bounded,

  • \(\sup F\) exists

  • \(\exists\) a sequence \(\{x_n\} \subset F\) with \(x_n \to \sup F\)

Since \(F\) is closed, this implies that \(\sup F \in F\)

Hence \(\max F\) exists and \(\max F = \sup F\)

Segway to functions#

Of course, in optimization we are mainly interested in maximizing and minimizing functions

Will apply the notions of supremum and infimum, minimum and maximum to the range of a function

\[\text{From} \quad A \subset \mathbb{R} \quad \text{go to} \quad \mathrm{rng}(f) \subset \mathbb{R}, \; f \colon X \subset \mathbb{R}^N \to \mathbb{R}\]

Equivalently, we may consider the image of a set \(X \subset \mathbb{R}^N\) under a function \(f\)

\[f(X) = \{ f(x) \colon x \in X\}\]

Definition

Let \(f \colon A \to \mathbb{R}\), where \(A\) is any set

The supremum of \(f\) on \(A\) is defined as

\[\sup_{x \in A} f(x) = \sup f(A)\]

The infimum of \(f\) on \(A\) is defined as

\[\inf_{x \in A} f(x) = \inf f(A)\]
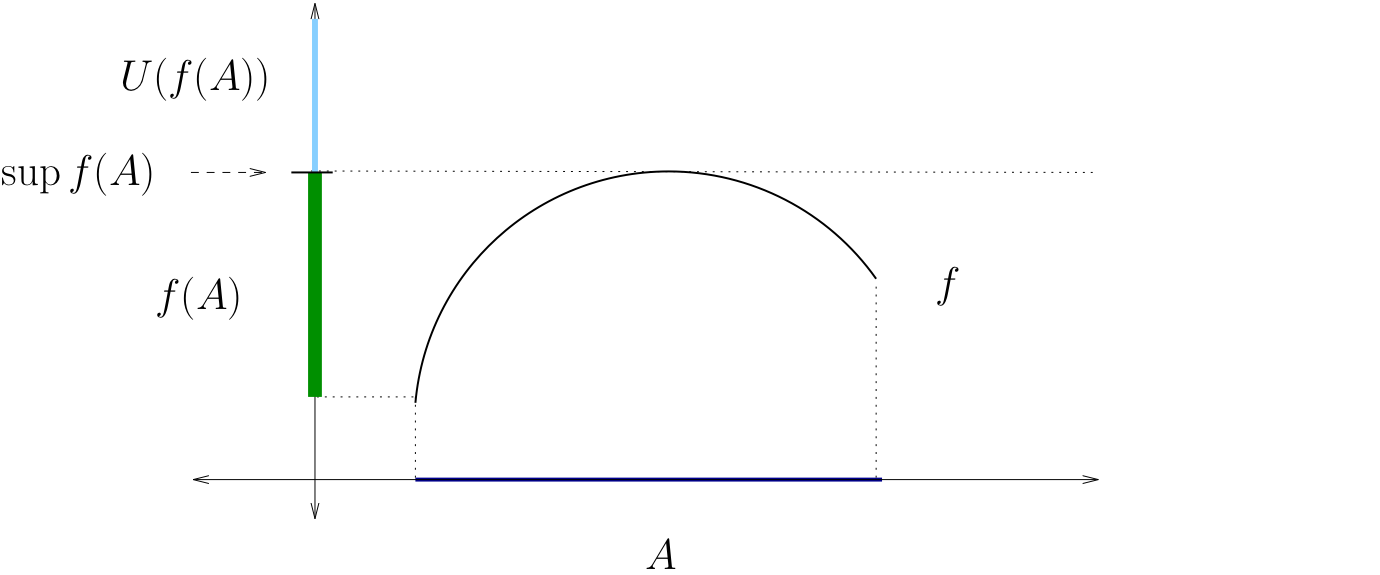
_images/func_sup.png

Fig. 41 The supremum of \(f\) on \(A\)#

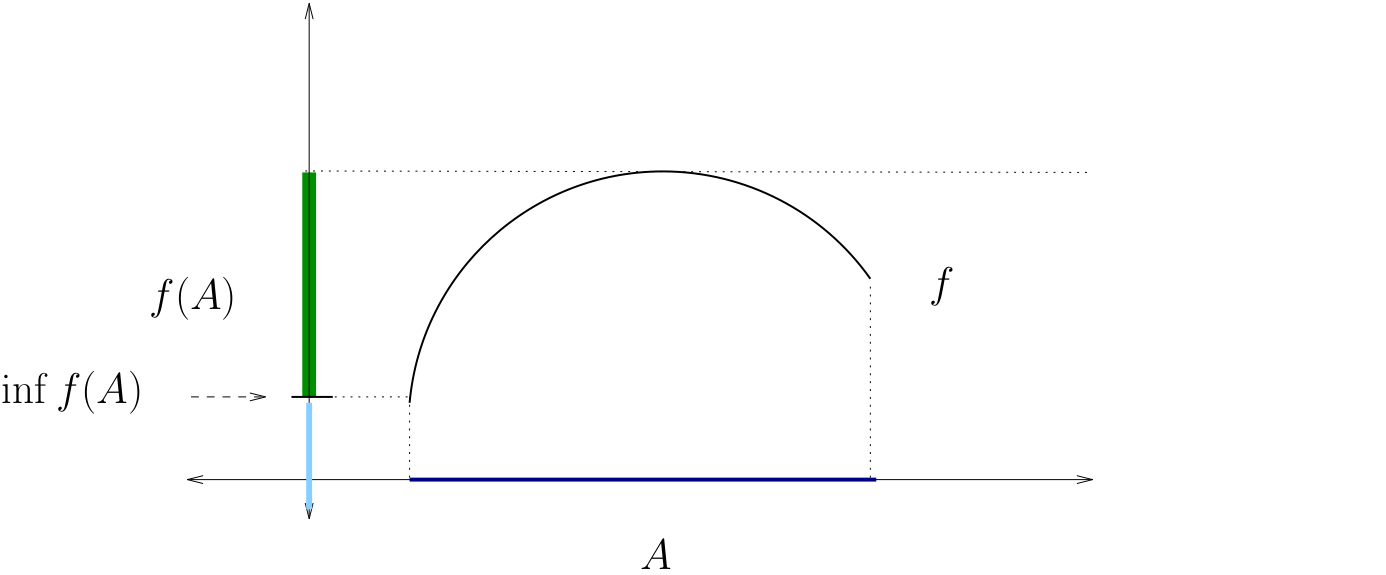
_images/func_inf.png

Fig. 42 The infimum of \(f\) on \(A\)#

Definition

Let \(f \colon A \to \mathbb{R}\) where \(A\) is any set

The maximum of \(f\) on \(A\) is defined as

\[\max_{x \in A} f(x) = \max f(A)\]

The minimum of \(f\) on \(A\) is defined as

\[\min_{x \in A} f(x) = \min f(A)\]

$$

Definition

A maximizer of \(f\) on \(A\) is a point \(a^* \in A\) such that

\[a^* \in A \text{ and } f(a^*) \geqslant f(x) \text{ for all } x \in A, \quad \text{alternatively}\]
\[f(a^*) = \max_{x \in A} f(x)\]

The set of all maximizers is typically denoted by

\[\mathrm{argmax}_{x \in A}f(x)\]

Definition

A minimizer of \(f\) on \(A\) is a point \(a^* \in A\) such that

\[a^* \in A \text{ and } f(a^*) \leqslant f(x) \text{ for all } x \in A, \quad \text{alternatively}\]
\[f(a^*) = \min_{x \in A} f(x)\]

The set of all minimizers is typically denoted by

\[\mathrm{argmin}_{x \in A}f(x)\]

Weierstrass extreme value theorem#

Fundamental result on existence of maxima and minima of functions!

Fact (Weierstrass extreme value theorem)

If \(f: A \subset \mathbb{R}^N \to \mathbb{R}\) is continuous and \(A\) is closed and bounded,
then \(f\) has both a maximizer and a minimizer on \(A\).

Proof

Sketch of the proof:

  • If \(f\) is continuous and \(A\) is compact, then \(f(A)\) is bounded, see relevant fact

  • Because \(f(A)\) is bounded \(\sup f(A)\) and \(\inf f(A)\) exist, see relevant fact

  • There is a sequence \(\{y_n\} \in f(A)\) converging to sup/inf, see relevant fact

  • Consider the corresponding sequence of \(x\) such that \(y=f(x)\)

  • It may not be convergent, but is bounded (belongs to compact), therefore contains a convergent subsequence (by Bolzano-Weierstrass theorem), see relevant fact

  • Let \(c\) be the limit of a convergent subsequence

  • Then by definition of continuity \(f(c)\) is the limit of the sequence \(f(x_n)\)

  • \(f(c)\) must then be the same as the limit of the sequence \(y_n\) = sup/inf due to the fact that any sequence can have at most one limit, see relevant fact

  • Therefore sup/inf is attained at \(x=c\)

Example

Consider the problem

\[ % \max_{c_1, c_2} \; U(c_1, c_2) = \sqrt{c_1} + \beta \sqrt{c_2} % \]
\[ % \text{ such that } \; c_2 \leqslant (1 + r)(w - c_1), \quad c_i \geqslant 0 \text{ for } i = 1,2 % \]

where

  • \(r=\) interest rate, \(w=\) wealth, \(\beta=\) discount factor

  • all parameters \(> 0\)

Let \(B\) be all \((c_1, c_2)\) satisfying the constraint

Exercise: Show that the budget set \(B\) is a closed, bounded subset of \(\mathbb{R}^2\)

Exercise: Show that \(U\) is continuous on \(B\)

We conclude that a maximizer exists

References and further reading#

References

  • Simon & Blume: 12.2, 12.3, 12.4, 12.5, 13.4, 29.2, 30.1

  • Sundaram: 1.2.6, 1.2.7, 1.2.8, 1.2.9, 1.2.10, 1.4.1, section 3

Contents