Announcements & Reminders

• March 11, next Monday is the first online test (3% of final grade)

• 8:00 in the morning till 23:59

• Take only once, will need 20 min

• Will automatically submit after 20 min

• Compulsory!

• Will cover materials up to and including this lecture

• You will get email notification from Wattle

• There will be a practice test to help you familiarize yourself with the system

📖 Basic set theory

⏱ | words

Reminder about the notation

Notation	Meaning
\(P \implies Q\)	\(P\) implies \(Q\)
\(P \iff Q\)	\(P \implies Q\) and \(Q \implies P\)
\(\exists\)	there exists
\(\forall\)	for all [elements in a set]
\(a := \text{[expression]}\)	\(a\) is defined to be equal to \(\text{[expression]}\)
\(a \equiv \text{[expression]}\)	\(a\) is defined to be equal to \(\text{[expression]}\)
\(a \stackrel{def.}{=} \text{[expression]}\)	\(a\) is defined to be equal to \(\text{[expression]}\)
\(\in\)	is element of
\(\subset\)	is subset of
\(\cup\)	union
\(\cap\)	intersection

Naive set theory

Definition

A set (\(X\)) is a collection of objects.
A particular object within a set (\(x\)) is known as an element of that set.

• Sets: \(A, B, X\)

• Elements: \(x,y,z\)

• \(x \in X\) denotes the idea that x is an element of X

• \(y \notin X\) denotes the idea that y is not an element of X

• empty set is denoted by \(\varnothing\)

Definition of a set

A set \(A\) can be defined by either

• direct enumeration of its elements

• defining a formula for infinite number of elements

• as a subset of already defined set \(B\), formula \(\psi(x)\) to form elements of \(A\), and a condition/property on \(x\)

\[A = \{ \psi(x), x \in B \,\colon\, \text{condition on x}\}\]

Some common number sets

• The set of natural numbers:

\[\mathbb{N} = \{1, 2, 3, · · · \}\]

• The set of non-negative intergers:

\[\mathbb{Z}_+ = \{0, 1, 2, · · · \}\]

• The set of integers:

\[\mathbb{Z} = \{· · · , −2, −1, 0, 1, 2, · · · \}\]

• The set of rational numbers:

\[\mathbb{Q} = \{ \frac{m}{n} : m \in \mathbb{Z}, n \in \mathbb{N}\}\]

• The set of non-negative rational numbers:

\[\mathbb{Q}_+ = \{x \in \mathbb{Q} : x \geqslant 0\}\]

• The set of positive rational numbers:

\[\mathbb{Q}_{++} = \{x \in \mathbb{Q} : x > 0\}\]

• The set of real numbers:

\[\mathbb{R} = (-\infty, \infty) \text{ (all numbers on the real line)}\]

• The set of non-negative real numbers:

\[\mathbb{R}_+ = \{x \in \mathbb{R} : x \geqslant 0\}\]

• The set of positive real numbers:

\[\mathbb{R}_{++} = \{x \in \mathbb{R}: x > 0\}\]

• The set of complex numbers:

\[\mathbb{C} = \{ a + bi : a \in \mathbb{R}, \: b \in \mathbb{R}, \: i = \sqrt{−1} \}\]

Example

\[\begin{split}\begin{array}{ccc} 1 \in \mathbb{N} & 0 \in \mathbb{Z}_+ & -1 \in \mathbb{Z} \\ \frac{1}{2} \in \mathbb{Q} & \sqrt{2} \in \mathbb{R} & \sqrt{2} \in \mathbb{R}_{++} \end{array}\end{split}\]

Subsets

Definition

Suppose that every element of \(X\) also belongs to \(Y\). If this is the case, then we say that \(X\) is a subset of \(Y\).

This is written in mathematical notation as \(X \subseteq Y\)

Definition

Suppose that in addition to every element of \(X\) also belonging to \(Y\), there is at least one element of \(Y\) that does not belong to \(X\). If this is the case, then we say that \(X\) is a proper subset of \(Y\).

This is written is mathematical notation as \(X \subset Y\).

Sometimes \(X \subset Y\) is used (rather loosely) to mean \(X \subseteq Y\). If this meaning of the notation is employed, then \(X \subsetneq Y\) would need to be used to indicate that \(X\) is a proper subset of \(Y\).

Definition

Sets \(X\) and \(Y\) are equal, denoted \(X=Y\), if and only if simultaneously \(X \subset Y\) and \(Y \subset X\).

Fact

The following nested structure holds for the number sets

\[\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\]

Proof

Note that \(\mathbb{N} \subset \mathbb{Z}_+\) because \(\mathbb{Z}_+ = \mathbb{N} \cup \{0\}\).

Note that \(\mathbb{Z}_+ \subset \mathbb{Z}\) because \(\mathbb{Z} = \mathbb{Z}_+ \cup \{ · · · , −3, −2, −1 \}\).

Note that \(\mathbb{Z} \subset \mathbb{Q}\) because any \(m \in \mathbb{Z}\) can be written as \(\frac{m}{1}\) and \(1 \in \mathbb{N}\), but there are fractions that do not belong to Z (for example \(\frac{1}{2} \notin \mathbb{Z}\)).

Note that \(\mathbb{Q} \subset \mathbb{R}\) because \(\frac{m}{n} \in (−\infty, \infty)\) for all \(m \in \mathbb{Z}\) and \(n \in \mathbb{N}\), but there are numbers on the real line that cannot be expressed as fractions (for example \(\sqrt{2}\), \(\pi\) and \(e\)). Real numbers that cannot be expressed as fractions are known as “irrational numbers”.

Note that \(\mathbb{R} \subset \mathbb{C}\) because

\[\mathbb{R} = \{ a + bi : a \in \mathbb{R}, \: b = 0, \: i = \sqrt{−1} \}\]

and \(0 \in \mathbb{R}\), but \((a + bi) \notin \mathbb{R}\) if \(b \neq 0\).

Example

Common notation for the intervals of \(\mathbb{R}\):

\[\begin{split}\begin{array}{rcl} (a, b) & \equiv & \{ x \in \mathbb{R} : a < x < b \} \\ (a, b] & \equiv & \{ x \in \mathbb{R} : a < x \leq b \} \\ [a, b) & \equiv & \{ x \in \mathbb{R} : a \leq x < b \} \\ [a, b] & \equiv & \{ x \in \mathbb{R} : a \leq x \leq b \} \\ [a, \infty)& \equiv & \{ x \in \mathbb{R} : a \leq x \} \\ (-\infty, b)& \equiv & \{ x \in \mathbb{R} : x < b \} \end{array}\end{split}\]

Example

Set of all subsets of a set \(A=\{1,2,3\}\) is

\[2^A = \big\{\varnothing, \{1\} , \{2\} , \{3\} , \{1, 2\} , \{1, 3\} , \{2, 3\} , \{1, 2, 3\}\big\}\]

Definition

The power set \(2^X\) of a set \(X\) is the set of all subsets of \(X\).

Russell’s Paradox

It would be nice if we could always associate some type of set with any particular property that we might consider. In other words, it would be nice if for any property \(\mathbb{A}\), we could form a set \(\{x \in X : \mathbb{A}(x) \text{ is true}\}\) that consisted of all of the elements that satisfy this property. Unfortunately, this is not the case.

This was established by British philosopher and mathematician Bertrand Russell and published in 1901. He did this by developing the following paradox.

Let \(\mathbb{A}\) be the property “is a set and does not belong to itself”. Suppose that \(A\) is the set of all sets that possess property \(\mathbb{A}\). Is \(A \in A\)?

If \(A \in A\), then it must be the case that \(A\) possesses property \(\mathbb{A}\). This means that \(A \notin A\). Contradiction! Thus it must be the case that \(A \notin A\). But if \(A\) is a set and \(A \notin A\), then it clearly possesses property \(\mathbb{A}\). Thus \(A \in A\). Contradiction. Thus it must be the case that \(A \in A\).

We have a paradox. It cannot be the case that both \(A \in A\) and \(A \notin A\).

One possible resolution to Russell’s paradox is to not allow mathematical objects like this particular \(A\) to be considered a set. Re-definition of the set theory by Ernst Zermelo, Abraham Fraenkel and Thoralf Skolem in 1908-1920, known today as ZFC axiomatic set theory.

Operations on sets

Union and intersection

Suppose that U is some universal set, \(X \subseteq U\) and \(Y \subseteq U\).

Definition

The union of \(X\) and \(Y\), which is denoted by \(X \cup Y\), is the set

\[ X \cup Y = \{a \in U : a \in X \text{ or } a \in Y\} \]

Note that the “or” in this definition is not exclusive. If the element \(a\) belongs to either \(X\) only, or \(Y\) only, or both \(X\) and \(Y\) , then \(a \in X \cup Y\).

Definition

The intersection of \(X\) and \(Y\), which is denoted by \(X \cap Y\), is the set

\[ X \cap Y = \{a \in U : a \in X \text{ and } a \in Y\} \]

Definition

If \(X \cap Y = \varnothing\), then the sets \(X\) and \(Y\) are said to be disjoint.

Venn diagram: union of two (overlapping) sets

Relationships between sets can be visualized using Venn diagrams.

In this example, the red, brown and green areas are all part of \(A \cup B\): the union of set \(A\) (the left circle) and set \(B\) (the right circle).

Show code cell source Hide code cell source

from matplotlib import pyplot as plt
from matplotlib_venn import venn2, venn2_circles

v = venn2(subsets=(1, 1, 1))
v.get_label_by_id('10').set_text('')
v.get_label_by_id('01').set_text('')
v.get_label_by_id('11').set_text('')

c = venn2_circles(subsets=(1, 1, 1), linestyle = 'solid')

# Style options
plt.title("Union of two overlapping sets")

# Add bracket showing the union of the two sets
plt.annotate('A ∪ B', xy=(0.5, 0), xytext=(0.5, -0.1), xycoords='axes fraction', 
            fontsize=16, ha='center', va='top',
            bbox=dict(boxstyle='square', fc='white', color='k'),
            arrowprops=dict(arrowstyle='-[, widthB=9.5, lengthB=0.5', lw=2.0, color='k'))

plt.show()

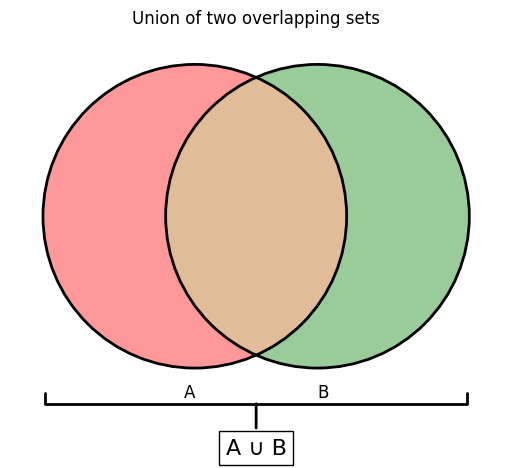
Venn diagram: intersection of two overlapping sets

The intersection of the two sets, \(A \cap B\), is the brown area.

Show code cell source Hide code cell source

from matplotlib import pyplot as plt
from matplotlib_venn import venn2, venn2_circles

v = venn2(subsets=(1, 1, 1))
v.get_label_by_id('10').set_text('')
v.get_label_by_id('01').set_text('')
v.get_label_by_id('11').set_text('$A \; ∩ \; B$')

c = venn2_circles(subsets=(1, 1, 1), linestyle = 'solid')

# Style options
plt.title("Intersection of two sets")

# Add legend
cols, texts = [],[]
cols.append(v.get_patch_by_id('11'))
texts.append(v.get_label_by_id('11')._text)
plt.legend(handles=cols, labels=texts, loc='upper right')

plt.show()

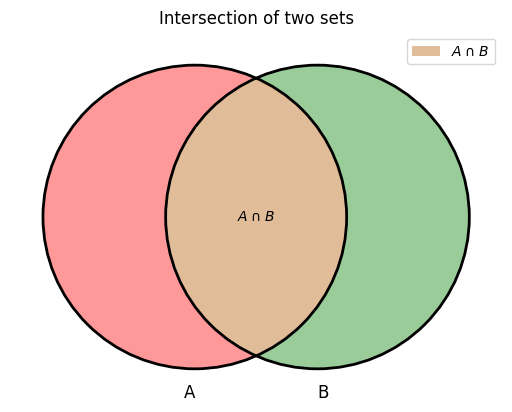
Venn diagram: intersection of two disjoint sets

In this diagram, \(A\) and \(B\) are disjoint sets. Therefore, \(A \cap B = \varnothing\).

Show code cell source Hide code cell source

from matplotlib import pyplot as plt
from matplotlib_venn import venn2, venn2_circles

v = venn2(subsets=(1, 1, 0))
v.get_label_by_id('10').set_text('')
v.get_label_by_id('01').set_text('')

c = venn2_circles(subsets=(1, 1, 0), linestyle = 'solid')

# Style options
plt.title("Intersection of disjoint sets is the empty set")

# Add legend
cols, texts = [],[]
for i in ('10', '01'):
    cols.append(v.get_patch_by_id(i))
    texts.append(v.get_label_by_id(i)._text)
# plt.legend(handles=cols, labels=texts)

plt.show()

Exclusion and complementation

Suppose that U is some universal set, \(X \subseteq U\) and \(Y \subseteq U\).

Definition

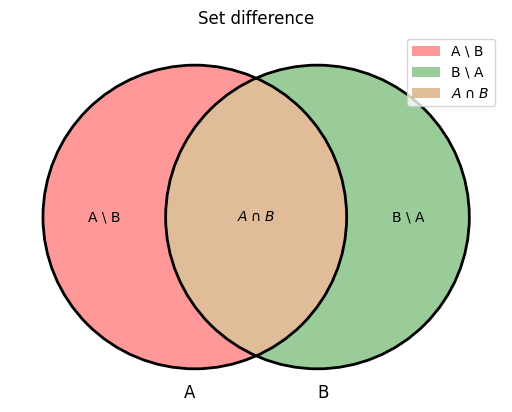
The set difference “X excluding Y”, which is denoted by \(X \setminus Y\), is the set

\[X \setminus Y = \{a \in X : a \notin Y \}\]

Definition

Set complementation is a special case of set exclusion. The complement of the set \(X\), which is denoted by \(X^C\) , is defined as \(X^C = U \setminus X\).

Note that \(X \cup X^C = U\) and \(X \cap X^C = \varnothing\).

Venn diagram: set difference

Show code cell source Hide code cell source

from matplotlib import pyplot as plt
from matplotlib_venn import venn2, venn2_circles

v = venn2(subsets=(1, 1, 1))
v.get_label_by_id('10').set_text('A \\ B')
v.get_label_by_id('01').set_text('B \\ A')
v.get_label_by_id('11').set_text('$A \; ∩ \; B$')

c = venn2_circles(subsets=(1, 1, 1), linestyle = 'solid')

# Style options
plt.title("Set difference")

# Add legend
cols, texts = [],[]
for i in ('10', '01', '11'):
    cols.append(v.get_patch_by_id(i))
    texts.append(v.get_label_by_id(i)._text)
plt.legend(handles=cols, labels=texts, loc='upper right')

plt.show()

Example

• \(\mathbb{Z} \setminus \mathbb{N} = \{\ldots, -2, -1, 0\}\)

• \(\mathbb{R} \setminus \mathbb{Q} = \) the set of irrational numbers

• \(\mathbb{R} \setminus [0, \infty) = (-\infty, 0)\)

• \(\mathbb{R} \setminus (a, b) = (-\infty, a] \cup [b, \infty)\)

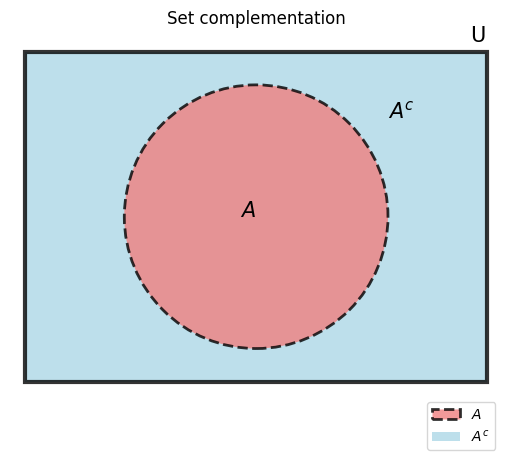
Venn diagram: set complementation

Notice that the large rectangle containing both \(A\) and \(A^c\) is labelled \(U\), the universal set.

Show code cell source Hide code cell source

from matplotlib import pyplot as plt
from matplotlib_venn import venn2, venn2_circles
from matplotlib.patches import Rectangle, Circle

fig, ax = plt.subplots()



ax.add_patch(Rectangle((-0.7, -0.5), 1.4, 1,
                       fc='lightblue',
                       alpha=0.8,
                       color='none',
                       linewidth=5))


ax.add_patch(Rectangle((-0.7, -0.5), 1.4, 1,
                       fc='none',
                       alpha=0.8,
                       color='black',
                       linewidth=3))


ax.add_patch(Circle((0, 0), 0.4,
                       fc='lightcoral',
                       alpha=0.8,
                       color='black',
                       linewidth=2,
                   linestyle='dashed'))

v = venn2(subsets=(1, 1, 1))
for i in ('10', '01', '11'):
    v.get_patch_by_id(i).set_alpha(0)
    v.get_label_by_id(i).set_text('')

v.get_label_by_id('A').set_text('')
v.get_label_by_id('B').set_text('')
    
# Style options
plt.title("Set complementation")

plt.text(0.65, 0.53, 'U', fontsize=15)
plt.text(-0.05, 0, '$A$', fontsize=15)
plt.text(0.4, 0.3, '$A^c$', fontsize=15)

cols, texts = [],[]
cols.append(ax.patches[2])
texts.append('$A$')
cols.append(ax.patches[0])
texts.append('$A^c$')

plt.legend(handles=cols, labels=texts, loc='lower right',
           bbox_to_anchor=(1, -0.15))


plt.show()

Example

\((a,\infty)^c\) generally understood to be \((-\infty, a]\)

Example: Set complement

Suppose that the universal set is \(U = \{1, 2, 3\}\). The power set for the set \(U\) in this example is

\[2^U = \{\varnothing, \{1\} , \{2\} , \{3\} , \{1, 2\} , \{1, 3\} , \{2, 3\} , \{1, 2, 3\}\} .\]

The elements of this power set are the subsets of the universal set. The complements for each of these subsets are:

• \(\varnothing^c = U\)

• \(\{1\}^c = \{2, 3\}\)

• \(\{2\}^c = \{1, 3\}\)

• \(\{3\}^c = \{1, 2\}\)

• \(\{1, 2\}^c = \{3\}\)

• \(\{1, 3\}^c = \{2\}\)

• \(\{2, 3\}^c = \{1\}\)

• \(U^c = \varnothing\)

Symmetric difference

Definition

The symmetric difference of \(X\) and \(Y\), which is denoted by \(X \bigtriangleup Y\), is the set

\[X \bigtriangleup Y = (X \setminus Y) \cup (Y \setminus X)\]

It is interesting to compare the operations of union and symmetric difference. They relate to alternative interpretions of the phrase “belongs to either \(X\) or \(Y\)”.

• The set \(X \cup Y\) consists of all elements that are either in set \(X\) only, or in set \(Y\) only, or in both of these sets.

• The set \(X \bigtriangleup Y\) consists of all elements that are either in set \(X\) only, or in set \(Y\) only, but are not in both of these sets.

Note

Exclusive or is another name for the symmetric difference operation.

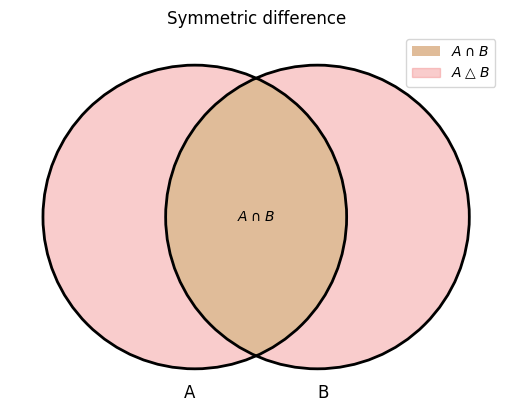
Venn diagram: symmetric difference

Note that the areas in light red together comprise the symmetric difference.

Show code cell source Hide code cell source

from matplotlib import pyplot as plt
from matplotlib_venn import venn2, venn2_circles

v = venn2(subsets=(1, 1, 1))
v.get_label_by_id('10').set_text('')
v.get_label_by_id('01').set_text('')
v.get_label_by_id('11').set_text('$A \; ∩ \; B$')

v.get_patch_by_id('01').set_color('lightcoral')
v.get_patch_by_id('10').set_color('lightcoral')


c = venn2_circles(subsets=(1, 1, 1), linestyle = 'solid')

# Style options
plt.title("Symmetric difference")

# Add legend
cols, texts = [],[]
cols.append(v.get_patch_by_id('11'))
texts.append(v.get_label_by_id('11')._text)
cols.append(v.get_patch_by_id('10'))
texts.append('$A \; △ \; B$')
plt.legend(handles=cols, labels=texts, loc='upper right')

plt.show()

Set operations properties

If \(A\) and \(B\) subsets of \(S\), then

1. \(A \cup B = B \cup A\) and \(A \cap B = B \cap A\)

• \((A \cup B)^c = B^c \cap A^c\) and \((A \cap B)^c = B^c \cup A^c\)

• \(A \setminus B = A \cap B^c\)

9. \((A^c)^c = A\)

Definition

If \(A \cap B = \emptyset\), then \(A\) and \(B\) said to be disjoint

Infinite Unions and Intersections

Given a family of sets \(K_{\lambda} \subset S\) with \(\lambda \in \Lambda\),

\[ \bigcap_{\lambda \in \Lambda} K_{\lambda} := \{ x \in S : x\in K_{\lambda} \textnormal{ for all } \lambda \in \Lambda \} \]

\[ \bigcup_{\lambda \in \Lambda} K_{\lambda} := \{x \in S \colon \textnormal{there exists an } \lambda \in \Lambda \textnormal{ such that } x\in K_{\lambda} \} \]

• “there exists” means “there exists at least one”

• denoted \(\exists\)

Fact

Let \(A := \cap_{n \in \mathbb{N}} (0, 1/n)\). Then \(A = \emptyset\).

Proof

We need to show that \(A\) contains no elements

Suppose to the contrary that \(x \in A = \cap_{n \in \mathbb{N}} (0, 1/n)\)

Then \(x\) is a number satisfying \(0 < x < 1/n\) for all \(n \in \mathbb{N}\)

Let’s prove by contradiction that such number does not exist

• Suppose to the contrary that such an \(x\) does exist

• \(x > 0\) \(\implies\) \(1/x < \infty\)

• Let \(k\in \mathbb{N}\) be the smallest integer such that \(k \geq 1/x\)

• Then we also have \(1/k \leq x\)

• This contradicts the initial assumption that \(x < 1/n\) for all \(n \in \mathbb{N}\)!

We have a contradiction, implying that there is no such \(0 < x < 1/n\) for all \(n \in \mathbb{N}\), and hence \(A = \emptyset\) \(\blacksquare\)

Example

For any \(a < b\) we have \(\cup_{\epsilon > 0 } \; [a + \epsilon, b) = (a, b)\)

Proof

To show equality of the sets, we show that RHS \(\subset\) LHS and LHS \(\subset\) RHS

Pick any \(a < b\)

Suppose first that \(x \in \cup_{\epsilon > 0 } \; [a + \epsilon, b)\)

This means there exists \(\epsilon > 0\) such that \(a + \epsilon \leq x < b\)

Clearly \(a < x < b\), and hence \(x \in (a, b)\)

Conversely, if \(a < x < b\), then \(\exists \, \epsilon > 0\) s.t. \(a + \epsilon \leq x < b\)

Hence \(x \in \cup_{\epsilon > 0 } \; [a + \epsilon, b)\)

Fact: de Morgan’s laws

Let \(S\) be any set and let \(K_{\lambda} \subset S\) for all \(\lambda \in \Lambda\). Then

\[ \left[ \bigcup_{\lambda \in \Lambda} K_{\lambda} \right]^{c} = \bigcap_{\lambda \in \Lambda} K_{\lambda}^{c} \quad \text{and} \quad \left[ \bigcap_{\lambda \in \Lambda} K_{\lambda} \right]^{c} = \bigcup_{\lambda \in \Lambda} K_{\lambda}^{c} \]

Proof

Let’s prove that \(A := \left( \cup_{\lambda \in \Lambda} K_{\lambda} \right)^{c} = \cap_{\lambda \in \Lambda} K_{\lambda}^{c} =: B\)

Suffices to show that \(A \subset B\) and \(B \subset A\)

Let’s just do \(A \subset B\)

Must show that every \(x \in A\) is also in \(B\)

Fix \(x \in A\)

Since \(x \in A\), it must be that \(x\) is not in \(\cup_{\lambda \in \Lambda} K_{\lambda}\)

\[ \text{therefore } \text{ $x$ is not in any $K_{\lambda}$ } \]

\[ \text{therefore } x \in K_{\lambda}^c \text{ for each } \lambda \in \Lambda \]

\[ \text{therefore } x \in \cap_{\lambda \in \Lambda} K_{\lambda}^{c} =: B \]

Necessary and sufficient conditions as set inclusion

Implications can be thought of as set inclusions

Equivalent forms of \(P \implies Q\):

1. If \(P\) is true then \(Q\) is true

2. \(P\) is a sufficient condition for \(Q\)

3. \(Q\) is a necessary condition for \(P\)

4. If \(Q\) fails then \(P\) fails

5. \(P \subset Q\)

Equivalent ways of saying \(P \nRightarrow Q\) (does not imply):

1. \(P\) does not imply \(Q\)

2. \(P\) is not sufficient for \(Q\)

3. \(Q\) is not necessary for \(P\)

4. Even if \(Q\) fails, \(P\) can still hold

5. \(P \not \subset Q\)

Tuples

We often organize collections with natural order into sets with fixed order of elements

Definition

A tuple is

• a finite ordered sequence of terms

• denoted using notation such as \((a_1, a_2)\) or \((x_1, x_2, x_3)\)

Example

Coordinates of a point in an Euclidean plane.

Example

Flip a coin 10 times and let

Let \(0\) represent tails and \(1\) represent heads, typical outcome \((1, 1, 0, 0, 0, 0, 1, 0, 1, 1)\)

Generic outcome \((b_1, b_2, \ldots, b_{10})\) for \(b_n \in \{0, 1\}\) are tuples

Cartesian Products

We make collections of tuples using Cartesian products

Definition

The Cartesian product of \(A_1, \ldots, A_N\) is the set

\[ A_1 \times \cdots \times A_N := \{ (a_1, \ldots, a_N) : a_n \in A_n \text{ for } n =1, \ldots, N \} \]

Example

\[ [0, 8] \times [0, 1] = \{ (x_1,x_2) : 0 \leq x_1 \leq 8, \, 0 \leq x_2 \leq 1 \} \]

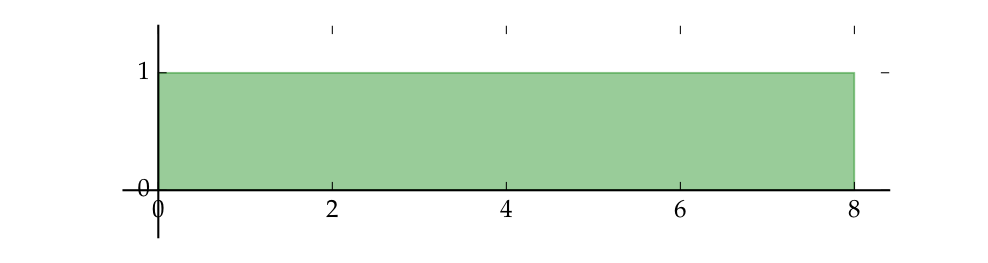
Example

Set of all outcomes from flip experiment is

\[ B := \Big\{ (b_1, \ldots, b_{10}) : b_n \in \{0, 1\} \text{ for } n = 1, \ldots, 10 \Big\} \]

\[ = \{0, 1\} \times \cdots \times \{0, 1\} \quad (10 \text{ products}) \]

Example

The standard two-dimensional Euclidean coordinate plane from high school:

\[\mathbb{R}^2 = \mathbb{R} \times \mathbb{R} = \{(x, y) : x \in \mathbb{R}, \; y \in \mathbb{R}\}\]

Also

\[\mathbb{R}^N = \mathbb{R} \times \cdots \times \mathbb{R} \quad (N \text{ times}) = \{ \, \text{all tuples } (x_1, \ldots, x_N) \text{ with } x_n \in \mathbb{R} \}\]

Example

If X = {1, 2, 3}, then the Cartesian product of X with itself is given by

\[X^2 = X \times X = \{(x, y) : x \in X , \; y \in X \}\]

• This set can also be written out as an exhaustive list of possible cases as follows:

\[X^2 = \{(1, 1) , (1, 2) , (1, 3) , (2, 1), (2, 2) , (2, 3) , (3, 1) , (3, 2) , (3, 3)\}\]

Counting Finite Sequences

Counting methods answer common questions such as

• How many arrangements of a sequence?

• How many subsets of a set?

They also address deeper problems such as

• How “large” is a given set?

• Can we compare size of sets even when they are infinite?

The key rule is: multiply possibilities

Example

Can travel from Sydney to Tokyo in 3 ways and Tokyo to NYC in 8 ways \(\implies\) can travel from Sydney to NYC in 24 ways

Example

Number of 10 letter passwords from the lowercase letters a,b,...,z is

\[26^{10} = 141,167,095,653,376\]

Example

Number of possible distinct outcomes \((i, j)\) from 2 rolls of a dice is

\[6 \times 6 = 36\]

Counting Cartesian Products

Definition

The number of elements in a finite set \(X\) can be denoted by either

• \(\# X\)

• \(|X|\)

• \(nX\)

• \(n(X)\)

Fact

If \(A_n\) are finite for \(n=1, \ldots,N\), then

\[\#(A_1 \times \cdots \times A_N) = (\# A_1) \times \cdots \times (\# A_N)\]

That is, number of possible tuples \(=\) product of the number of possibilities for each element

Example

Number of binary sequences of length \(10\) is

\[\# [\{0, 1\} \times \cdots \times \{0, 1\}] = 2 \times \cdots \times 2 = 2^{10}\]

Infinite Cartesian Products

If \(\{A_n\}\) is a collection of sets, one for each \(n \in \mathbb{N}\), then

\[A_1 \times A_2 \times \cdots := \{ (a_1, a_2, \ldots) : a_n \in A_n \text{ for each } n \in \mathbb{N} \}\]

Sometimes denoted \(\times_{n=1}^{\infty} A_n\)

If \(A_n = A\) for all \(n\), then \(\times_{n=1}^{\infty} A\) also written as \(A^{\mathbb{N}}\)

Example

The set of all binary sequences \(\{0, 1\}^{\mathbb{N}}\)

References and further reading

References

• [Simon and Blume, 1994]: Appendix A1.1, A1.2

• [Sundaram, 1996]: Section 1.2.10, Appendix A.1, B.1

Further reading and self-learning

• Veritasium video on paradoxes of set theory and mathematical incompleteness YouTube