EXTRA MATERIAL

Material in this section is optional and will not be part of the course assessment.

☕️ Maximum theorem

⏱ | words

Also called The theorem of maximum and Berge's Maximum Theorem

Value function and parameters of optimization problems

Let’s start with recalling the definition of a general optimization problem

Definition

The general form of the optimization problem is

\[\begin{split} V(\theta) = \max_{x} f(x,\theta) \\ \text {subject to} \\ g_i(x,\theta) = 0, \; i\in\{1,\dots,I\}\\ h_j(x,\theta) \le 0, \; j\in\{1,\dots,J\} \end{split}\]

where:

• \(f(x,\theta) \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\) is an objective function

• \(x \in \mathbb{R}^N\) are decision/choice variables

• \(\theta \in \mathbb{R}^K\) are parameters

• \(g_i(x,\theta) = 0, \; i\in\{1,\dots,I\}\) where \(g_i \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\), are equality constraints

• \(h_j(x,\theta) \le 0, \; j\in\{1,\dots,J\}\) where \(h_j \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\), are inequality constraints

• \(V(\theta) \colon \mathbb{R}^K \to \mathbb{R}\) is a value function

This lecture focuses on the value function in the optimization problem \(V(\theta)\), and how it depends on the parameters \(\theta\).

In economics we are interested how the optimized behavior changes when the circumstances of the decision-making process change

• income/budget/wealth changes

• intertemporal effects of changes in other time periods

We would like to establish the properties of the value function \(V(\theta)\):

• continuity \(\rightarrow\) The maximum theorem

• changes/derivative (if differentiable) \(\rightarrow\) Envelope theorem

• monotonicity \(\rightarrow\) Supermodularity and increasing differences (not covered here, see Sundaram ch.10)

Main idea for the maximum theorem

When the components of the optimization problem \(f(x,\theta)\), \(g_i(x,\theta)\) and \(h_j(x,\theta)\) are continuous, then the value function \(V(\theta)\) is also continuous, in certain sense

We need to accurately define the notion of continuity for all components of the optimization problem

• objective function

• constraints \(\leftrightarrow\) admissible set

Denote the admissible set \(\mathcal{D}(\theta)\)

\[ \mathcal{D}(\theta) = \left\{ x \in \mathbb{R}^N \colon g_i(x,\theta) = 0, \; i\in\{1,\dots,I\}, \; h_j(x,\theta) \le 0, \; j\in\{1,\dots,J\} \right\} \]

In solving the optimization problem we are not only interested in the attainable optimal value \(V(\theta)\), but also in the set of maximizers/minimizers \(\mathcal{D}^\star(\theta)\) corresponding to each parameter value \(\theta\)

Definition

We will refer to the pair

\[\begin{split} V(\theta) = \max_{x} f(x,\theta) \\ \mathcal{D}^\star(\theta) = \mathrm{arg}\max_x f(x,\theta) \end{split}\]

as the solution of the optimization problem

\[\begin{split} f(x,\theta) \to \max_{x} \\ \text{subject to} \; x \in \mathcal{D}(\theta), \end{split}\]

where

\[\begin{split} \begin{array}{l} f(x,\theta) \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R},\\ \mathcal{D}(\theta) \subset \mathbb{R}^N \text{ for all } \theta,\\ \theta \in \Theta \subset \mathbb{R}^K \end{array} \end{split}\]

Correspondences

Note that the mappings of \(\theta\) to \(\mathcal{D}(\theta)\) or \(\mathcal{D}^\star(\theta)\) are not functions because both \(\mathcal{D}(\theta)\) and often \(\mathcal{D}^\star(\theta)\) have multiple elements for a given \(\theta\)

Definition

A correspondence (set-valued function) is a map that associates elements of its domain to sets of elements in its range, i.e.

\[ f \colon \Theta \subset \mathbb{R}^K \to P(\mathbb{R}^N) \]

where \(P(\mathbb{R}^N)\) denotes the power set of \(\mathbb{R}^N\), i.e. the set of all subsets of \(\mathbb{R}^N\). It can also be denoted as \(2^{\mathbb{R}^N}\).

Example

Let correspondence \(\Phi\) be defined as

\[ \Phi \colon \theta \in \Theta \subset \mathbb{R}^K \to \mathcal{D}(\theta) \subset P(\mathbb{R}^N) \]

Example

\[ \phi \colon x \in [0,1] \mapsto \{0,1\} \]

\[ \phi \colon x \in [0,1] \mapsto (0,1) \]

\[ \phi \colon x \in [0,1] \mapsto [0,1] \]

\[ \phi \colon x \in [0,1] \mapsto [x,1] \]

\[ \phi \colon x \in [0,1] \mapsto (0,1/x] \]

\[ \phi \colon x \in (0,1] \mapsto (0,1/x] \]

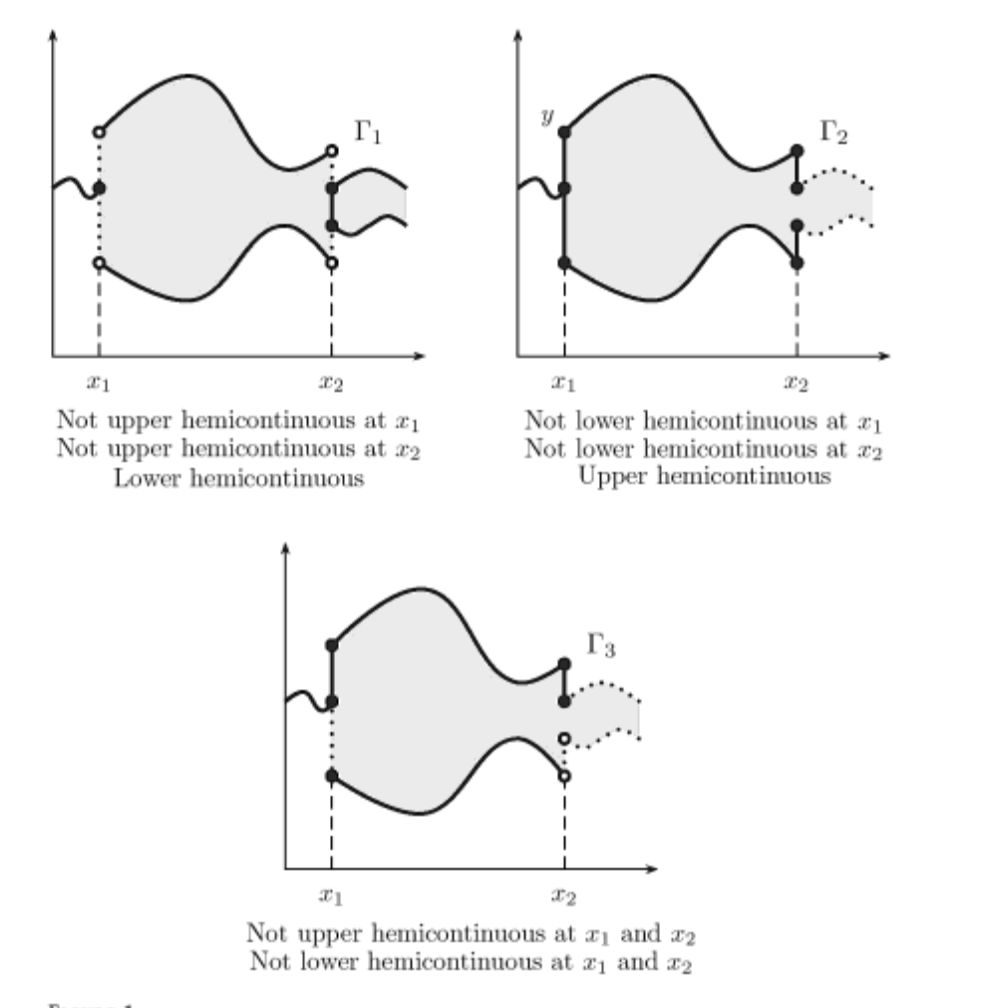
Fig. 102 Examples of correspondences (for labels see below)

Correspondences are classified by the properties of the sets they output:

• open-valued correspondences

• closed-valued correspondences

• non-empty-valued correspondences

• bounded-valued correspondences

• convex-valued correspondences

• compact-valued correspondences

• finite-valued correspondences

• singleton-valued correspondences (functions?)

Continuity of correspondences

Recall the definition of the continuous function

Definition

Function \(f \colon A \subset \mathbb{R}^n \to \mathbb{R}^m\) is called continuous at \({\bf x} \in A\) if as \(n \to \infty\) for every converging to \({\bf x}\) sequence

\[ {\bf x}_n \to {\bf x} \quad \implies \quad f({\bf x}_n) \to f({\bf x}) \]

The equivalent definition of continuity relies on the the open epsilon-balls

Fact

A function \(f \colon A \subset \mathbb{R}^n \to \mathbb{R}^m\) is continuous at \({\bf x} \in A\) if and only if for every \(\epsilon >0\) there is a \(\delta>0\) such that

\[ {\bf x}' \in B_\delta({\bf x}) \implies f({\bf x}') \in B_\epsilon(f({\bf x})) \]

Proof

Omitted here, but see https://www.u.arizona.edu/~mwalker/MathCamp2020/ContinuousFunctions.pdf

Thinking of the definition of limit stated in terms of open epsilon-balls, it is not hard to see the equivalence result

Generalization to correspondences is not straightforward because \(\in\) operation does not convert to the set-valued case immediately:

• can be replaced by set inclusion \(\subset\)

• can be represented by non-empty intersection \(\bar{\cap}\), i.e. \(A \bar{\cap} B \iff A \cap B \ne \emptyset \)

Namely, the condition in the definition above can be replaced with either

• \({\bf x}' \in B_\delta({\bf x}) \implies f({\bf x}') \subset B_\epsilon(f({\bf x}))\), or

• \({\bf x}' \in B_\delta({\bf x}) \ne \emptyset \implies f({\bf x}') \cap B_\epsilon(f({\bf x})) \ne \emptyset\)

Definition

Correspondence \(\gamma \colon X \to 2^Y\) is called upper hemi-continuous (uhc) at \({\bf x} \in X\) if for every open set \(V\) containing \(f({\bf x})\), i.e. \(f({\bf x}) \subset V\), there is an open set \(U\) such that

\[ {\bf x} \in U \text{ and } {\bf x}' \in U \implies f({\bf x}') \subset V \]

Correspondence \(\gamma \colon X \to 2^Y\) is called lower hemi-continuous (lhc) at \({\bf x} \in X\) if for every open set \(V\) intersecting with \(f({\bf x})\), i.e. \(f({\bf x}) \cap V \ne \emptyset\), there is an open set \(U\) such that

\[ {\bf x} \in U \text{ and } {\bf x}' \in U \implies f({\bf x}') \cap V \ne \emptyset \]

Definition

A corresponse is called continous if it is both upper and lower hemi-continuous

Note

Semi-continuity is a special notion of continuity for functions, and may be used as equivalent to hemi-continuity for correspondences

Examples, examples, examples (whiteboard)

Fact

Constant correspondences are both uhc and lhc

\[ \gamma \colon x \in X \mapsto \mathcal{D} \subset Y \text { for every } x \implies \gamma \text{ is continuous (uhc and lhc)} \]

Note

For closed-valued correspondences, a good rule of thumb for determining hemi-continuity at \({\bf x}\) is:

• if moving “a little amount” away from \({\bf x}\) no new points are “discontinuously/suddenly” appear outside of \(f({\bf x})\), \(f\) is uhc

• if moving “a little amount” away from \({\bf x}\) no points “suddenly” disappear from \(f({\bf x})\), \(f\) is lhc

The statement of the maximum theorem

Extremely useful in many fields of economics:

• demand (consumer) theory

• theory of the firm: supply of products, demand for inputs

• theory of economic growth

• game theory and industrial relations

The maximum theorem

Let \(f(x,\theta) \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\) be a continuous function, and \(\mathcal{D}(\theta)\) be a compact-valued continuous correspondence. Then the value function \(V(\theta)\) is continuous on \(\mathbb{R}^K\) and \(\mathcal{D}^\star(\theta)\) is a compact-valued upper hemi-continuous correspondence on \(\Theta\)

In other words, continuity of the fundamentals of the optimization problem are inherited by the value function, but not to the full extent (continuity \(\to\) hemi-continuity)

\[\begin{split} \begin{array}{l} \text{$f$ function continuous}\\ \text{$\theta \mapsto \mathcal{D}(\theta)$ compact-valued}\\ \text{$\theta \mapsto \mathcal{D}(\theta)$ continuous (uhc + lhc)} \end{array} \longrightarrow \begin{array}{l} V(\theta) \text{ continuous}\\ \mathcal{D}^\star(\theta) \text{ upper hemi-continuous} \end{array} \end{split}\]

Maximum theorem under convexity

Let \(f(x,\theta) \colon \mathbb{R}^N \times \mathbb{R}^K \to \mathbb{R}\) be a continuous function, and \(\mathcal{D}(\theta)\) be a compact-valued continuous correspondence. Then:

1. The value function \(V(\theta)\) is continuous on \(\mathbb{R}^K\) and \(\mathcal{D}^\star(\theta)\) is a compact-valued upper hemi-continuous correspondence on \(\Theta\) (as before)

2. If \(f(x,\theta)\) is concave in \(x\) and \(\mathcal{D}(\theta)\) is convex-valued for every \(\theta\), then \(\mathcal{D}^\star(\theta)\) is a convex-valued.
   If concavity of \(f(x,\theta)\) is strict, then \(\mathcal{D}^\star(\theta)\) is a singleton-valued upper hemi-continuous correspondence, hence a continuous function

3. If \(f\) is concave in \((x,\theta)\) and the graph of \(\mathcal{D}(\theta)\) is convex, in addition to the above the value function \(V(\theta)\) is concave. Under strict concavity \(V(\theta)\) is also strictly concave.

Definition

The graph of a correspondence \(\gamma \colon X \to 2^Y\) is defined as the set \(\{(x,y) \in X \times Y \colon y \in f(x)\}\)

Consider a special case for when the optimizer is unique for each \(\theta\)

Fact

A single-valued correspondence that is hemi-continuous (either uhc or lhc) is continuous when viewed as a function. Conversely, every continuous function, when viewed as a single-valued correspondence, is both uhc and lhc.

In this case the upper semi-continuity, lower semi-continuity coincide with the “usual” continuity

Example

Budget correspondence in the two goods consumer optimization problem. Assuming \(p_1>0,\, p_2>0,\, m>0\), the budget correspondence can be defined as

\[ \beta \colon (p_1,p_2,m) \mapsto \{(x_1,x_2) \in \mathbb{R}^2 \colon \forall i\; x_i \ge 0, p_1 x_1 + p_2 x_2 \leq m\} \]

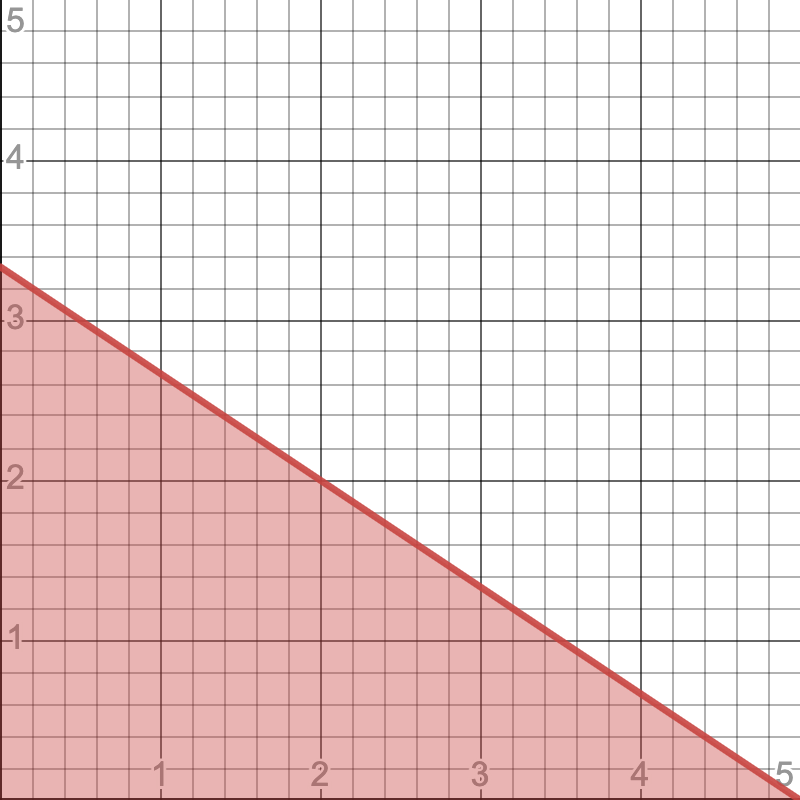
See online animation

Fact

Budget correspondence \(\beta\) defined above is both uhc and lhc, and therefore continuous

Example

Maximization of log utility subject to budget constraint

\[\begin{split} u(x_1, x_2) = \alpha \log(x_1) + \beta \log(x_2) \to \max_{x_1, x_2} \\ \text{ subject to} \\ p_1 x_1 + p_2 x_2 \leq m \end{split}\]

• \(p_i\) is the price of good \(i\), \(p_i>0\)

• \(m\) is the budget, assumed non-negative

• \(\alpha>0\), \(\beta>0\)

• \(x_1 \geq 0, \; x_2 \geq 0\), can show that these constraints never bind

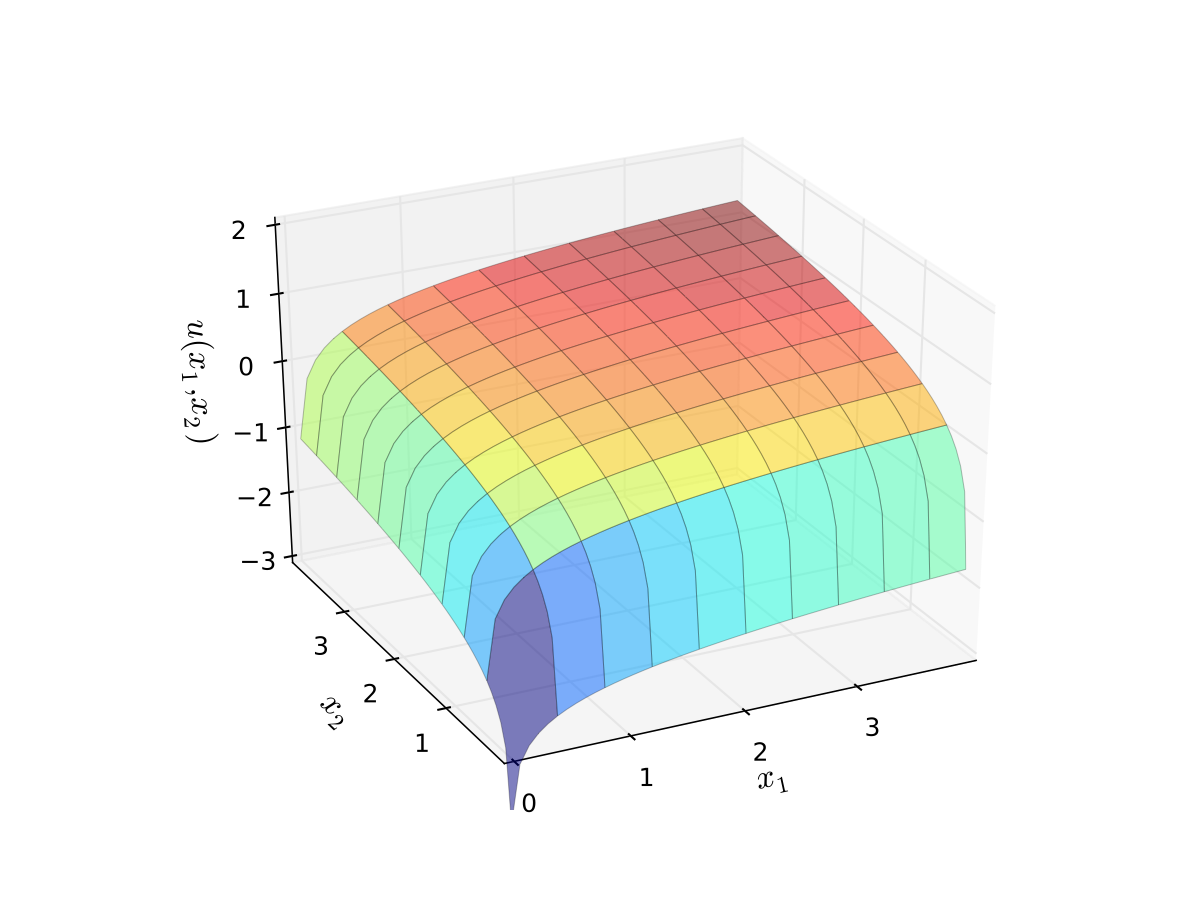
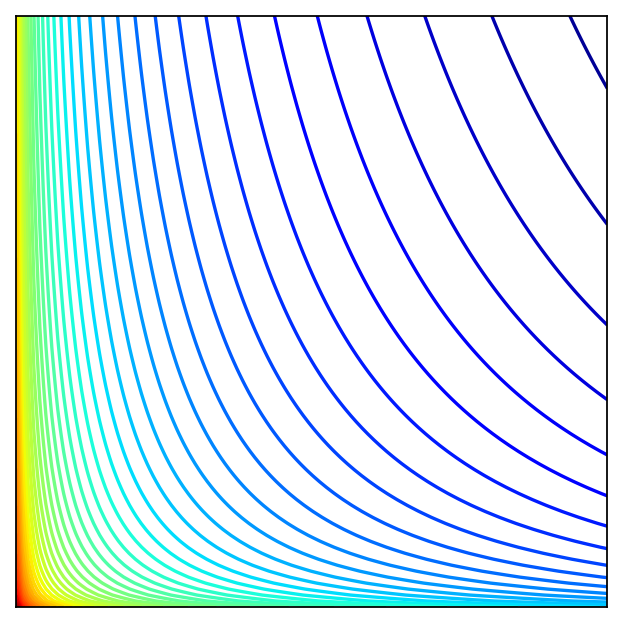
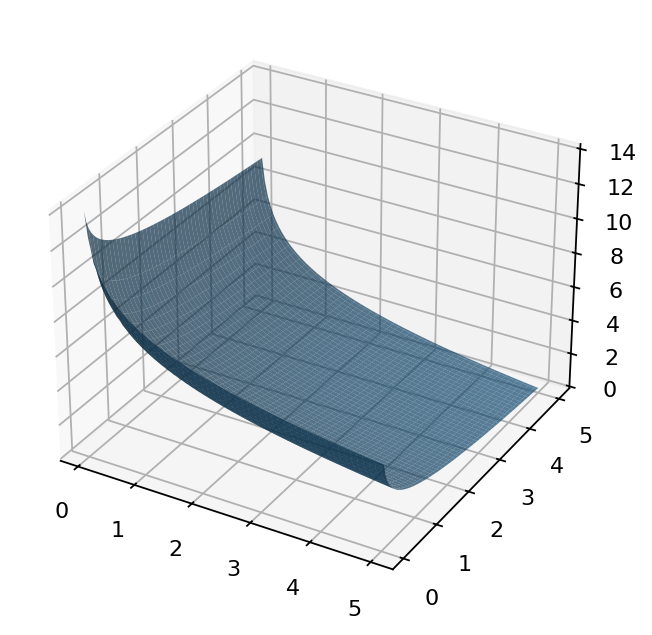
Fig. 103 Log utility with \(\alpha=0.4\), \(\beta=0.5\)

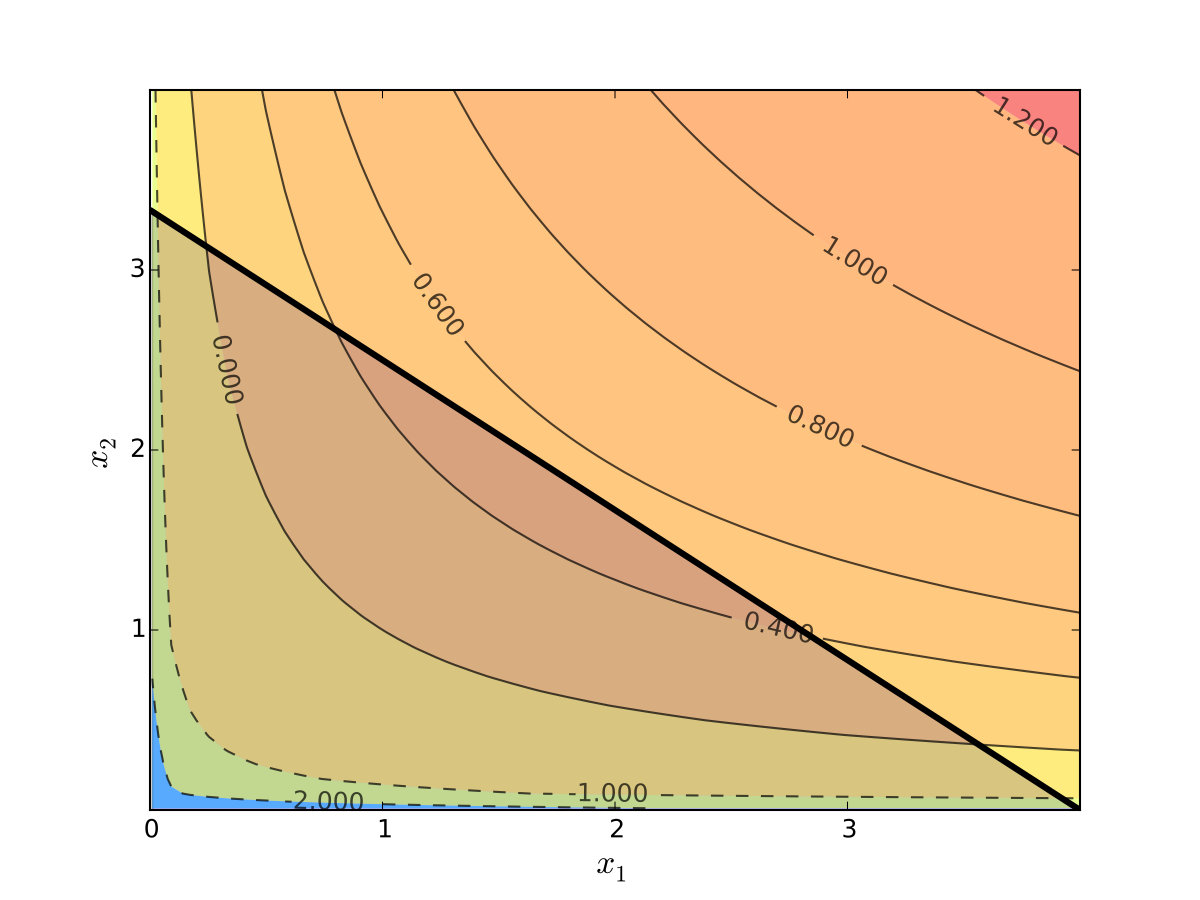
Fig. 104 Utility max for \(p_1=1\), \(p_2 = 1.2\), \(m=4\), \(\alpha=0.4\), \(\beta=0.5\)

The maximizer according to the FOC conditions and verified with SOC (see lecture 8) is

\[\begin{split} x_1^\star = \frac{\alpha}{\alpha + \beta} \cdot \frac{m}{p_1} \\ x_2^\star = \frac{\beta}{\alpha+\beta} \cdot \frac{m}{p_2} \end{split}\]

Applying the maximum theorem:

1. Objective function is continuous in all arguments

2. Constrained set is compact for all parameters (as they are defined)

3. Budget correspondence is continuous

Therefore the theorem applies and we have: the value function is continuous in all parameters, and the set of maximizers is upper hemi-continuous.

Moreover, we can show that the utility function is strictly concave for all parameters, therefore the clause 2 of the maximum theorem under convexity applies, and the set of maximizers is a singleton-valued correspondence, i.e. a function. We have already found it above.

We can verify that the value function is indeed continuous by plugging the maximizer back into the objective function

\[ V(p_1,p_2,m) = \alpha \log\left( \frac{\alpha}{\alpha + \beta} \cdot \frac{m}{p_1} \right) + \beta \log\left( \frac{\beta}{\alpha+\beta} \cdot \frac{m}{p_2} \right) \]

Question

Can \(\alpha\) and \(\beta\) be also considered as parameters in the previous analysis?

For the numerical example set \(\alpha = 2\), \(\beta = 1\), \(m = 10\), and let \(p_1\) and \(p_2\) vary

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

alpha = 2
beta = 1
m = 10
f = lambda x: alpha * np.log( alpha * m / ( (alpha+beta)*x[0] )) + beta * np.log( beta * m / ( (alpha+beta)*x[1] ))

lb,ub = .05,5

x = y = np.linspace(lb,ub, 100)
X, Y = np.meshgrid(x, y)
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)

fig = plt.figure(dpi=160)
ax2 = fig.add_subplot(111)
ax2.set_aspect('equal', 'box')
ax2.contour(X, Y, Z, 50,
            cmap=cm.jet)
plt.setp(ax2, xticks=[],yticks=[])

fig = plt.figure(dpi=160)
ax3 = fig.add_subplot(111, projection='3d')
ax3.plot_surface(X, Y, Z, 
            rstride=2, 
            cstride=2,
            alpha=0.7,
            linewidth=0.25)

plt.show()

Fig. 105 Value function in the space of prices \(p_1,p_2\)

Fig. 106 Value function in the space of prices \(p_1,p_2\)

Show code cell source Hide code cell source

alpha = 2
beta = 1
m = 10
# f = lambda x: alpha * np.log( alpha * m / ( (alpha+beta)*x[0] )) + beta * np.log( beta * m / ( (alpha+beta)*x[1] ))
f1 = lambda x: alpha * m / ( (alpha+beta)*x)
f2 = lambda x: beta * m / ( (alpha+beta)*x)

lb,ub = .5,5
x = np.linspace(lb,ub, 100)

fig = plt.figure(dpi=160)
ax = fig.add_subplot(111)
ax.plot(x,f1(x),label=r"$x_1^\star(p_1)$")
ax.plot(x,f2(x),label=r"$x_2^\star(p_2)$")
plt.legend(loc='upper right', frameon=False)
plt.show()

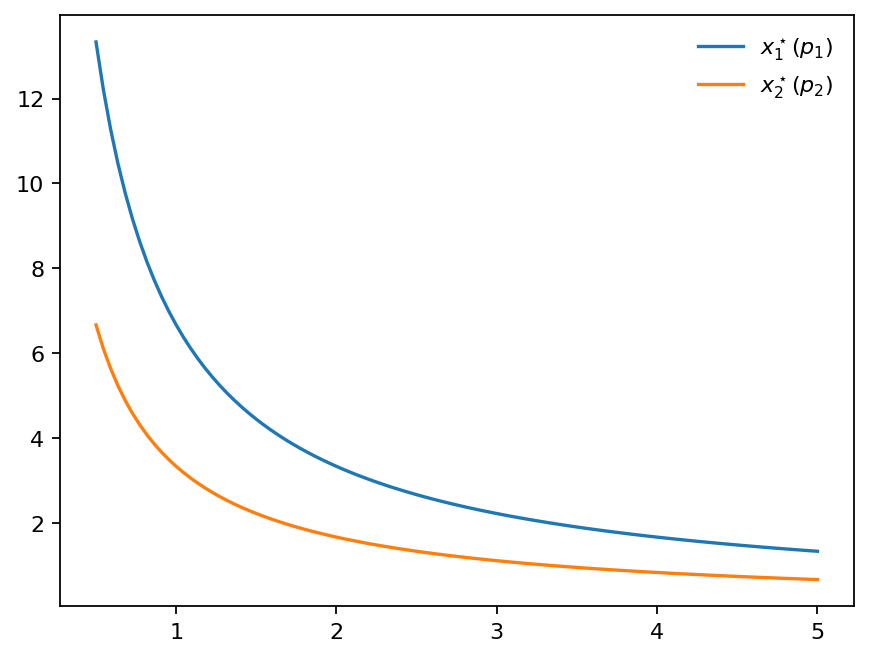
Fig. 107 Optimal choice of \(x_1\) and \(x_2\) as function of prices \(p_1\) and \(p_2\) (aka demand curve)

Example

Maximization of log-linear utility subject to budget constraint

\[\begin{split} u(x_1, x_2) = \alpha x_1 + \beta \log(x_2) \to \max_{x_1, x_2} \\ \text{ subject to} \\ p_1 x_1 + p_2 x_2 \leq m \\ x_1 \geq 0, \; x_2 \geq 0 \end{split}\]

• \(p_i\) is the price of good \(i\), assumed non-negative

• \(m\) is the budget, assumed non-negative

• \(\alpha>0\), \(\beta>0\)

Form the Lagrangian with 3 inequality constraints (have to flip the sign for non-negativity to stay within the general formulation)

\[\begin{split} \mathcal{L}(x_1,x_2,\lambda_1,\lambda_2,\lambda_3) = \\ = \alpha x_1 + \beta\log(x_2) - \lambda_1 (-x_1) - \lambda_2 (-x_2) - \lambda_3 (p_1 x_1 + p_2 x_2 -m) = \\ = \alpha x_1 + \beta\log(x_2) + \lambda_1 x_1+ \lambda_2 x_2 - \lambda_3 (p_1 x_1 + p_2 x_2 -m) \end{split}\]

The necessary KKT conditions are given by the following system of equations

\[\begin{split} \begin{cases} \frac{\partial \mathcal{L}}{\partial x_1} = 0 \implies \alpha + \lambda_1 - \lambda_3 p_1 = 0 \\ \frac{\partial \mathcal{L}}{\partial x_2} = 0 \implies \frac{\beta}{x_2} + \lambda_2 - \lambda_3 p_2 = 0 \\ x_1 \ge 0 \\ x_2 \ge 0 \\ x_1 p_1 + x_2 p_2 \le m \\ \lambda_1 \ge 0 \text { and } \lambda_1 x_1 = 0 \\ \lambda_2 \ge 0 \text { and } \lambda_2 x_2 = 0 \\ \lambda_3 \ge 0 \text { and } \lambda_3 (x_1 p_1 + x_2 p_2 -m) = 0 \\ \end{cases} \end{split}\]

The KKT conditions can be solved systematically by considering all combinations of the multipliers. The two cases where the system is consistent give the solution

\[\begin{split} \begin{cases} x_1^\star = \frac{m}{p_1} - \frac{\beta}{\alpha}, \; x_2^\star = \frac{\beta p_1}{\alpha p_2}, & \text{ if } p_1/m \le \alpha/\beta, \\ x_1^\star = 0, \; x_2^\star = \frac{m}{p_2}, & \text{ if } p_1/m > \alpha/\beta \\ \end{cases} \end{split}\]

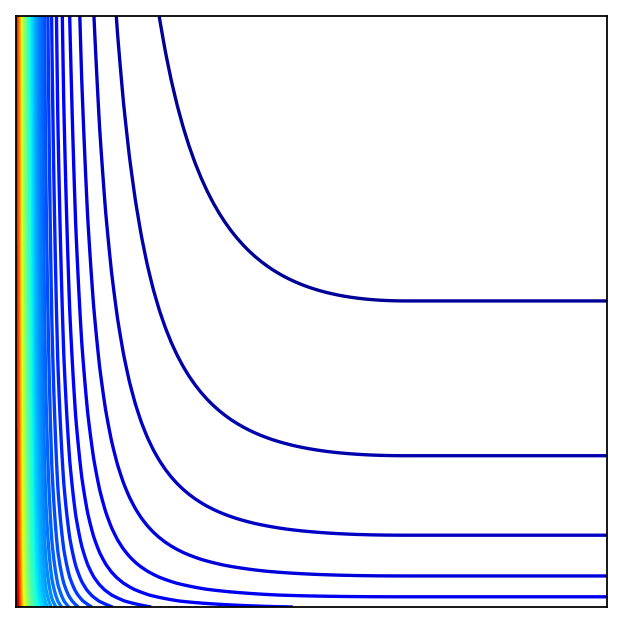
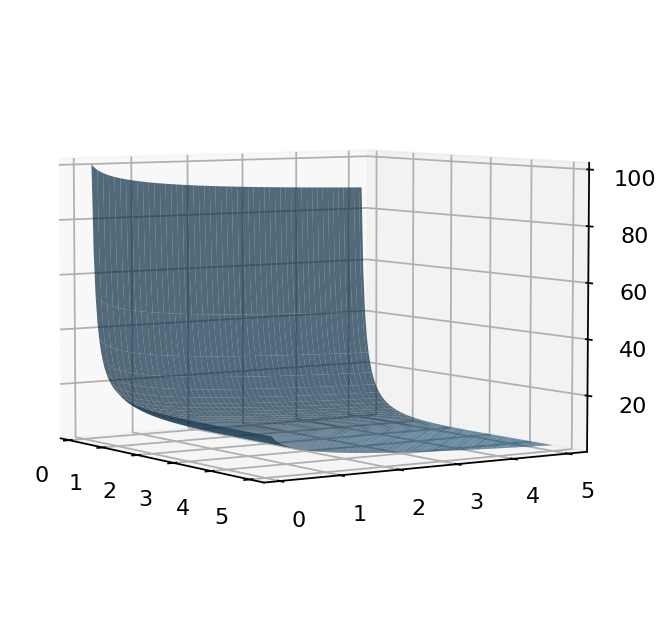
Fig. 108 Corner solution

Applying the maximum theorem:

1. Objective function is continuous in all arguments

2. Constrained set is compact for all parameters (as they are defined)

3. Budget correspondence is continuous

Therefore the theorem applies and we have: the value function is continuous in all parameters, and the set of maximizers is upper hemi-continuous.

Moreover, we can show that the utility function is strictly concave for all parameters, therefore the clause 2 of the maximum theorem under convexity applies, and the set of maximizers is a singleton-valued correspondence, i.e. a function. We have already found it above.

We can verify that the value function is indeed continuous by plugging the maximizer back into the objective function

\[\begin{split} V(p_1,p_2,m) = \begin{cases} \frac{\alpha m}{p_1} - \beta + \beta \log\left( \frac{\beta p_1}{\alpha p_2} \right), & \text{ if } p_1/m \le \alpha/\beta, \\ \beta \log\left( \frac{m}{p_2} \right), & \text{ if } p_1/m > \alpha/\beta \\ \end{cases} \end{split}\]

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

alpha = 1
beta = 3
m = 10
cond = lambda p1: p1/m <= alpha/beta
f = lambda p: cond(p[0])*( alpha * m / p[0] - beta + beta * np.log( beta * p[0] / ( alpha * p[1] )) ) + (1-cond(p[0])) * (beta * np.log( m / p[1] ))

lb,ub = .1,5

x = y = np.linspace(lb,ub, 100)
X, Y = np.meshgrid(x, y)
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)

fig = plt.figure(dpi=160)
ax2 = fig.add_subplot(111)
ax2.set_aspect('equal', 'box')
ax2.contour(X, Y, Z, 50,
            cmap=cm.jet)
plt.setp(ax2, xticks=[],yticks=[])

fig = plt.figure(dpi=160)
ax3 = fig.add_subplot(111, projection='3d')
ax3.plot_surface(X, Y, Z, 
            rstride=2, 
            cstride=2,
            alpha=0.7,
            linewidth=0.25)
ax3.view_init(elev=5, azim=-34)

plt.show()

Fig. 109 Value function in the space of prices \(p_1,p_2\)

Fig. 110 Value function in the space of prices \(p_1,p_2\)

Show code cell source Hide code cell source

alpha = 1
beta = 3
m = 10
cond = lambda p1: p1/m <= alpha/beta
f1 = lambda x: cond(x)*(m/x - beta/alpha) + (1-cond(x))*0
lb,ub = .5,10
x = np.linspace(lb,ub, 100)
fig = plt.figure(dpi=160)
ax = fig.add_subplot(111)
ax.plot(x,f1(x),label=r"$x_1^\star(p_1)$")
plt.legend(loc='upper right', frameon=False)
plt.show()

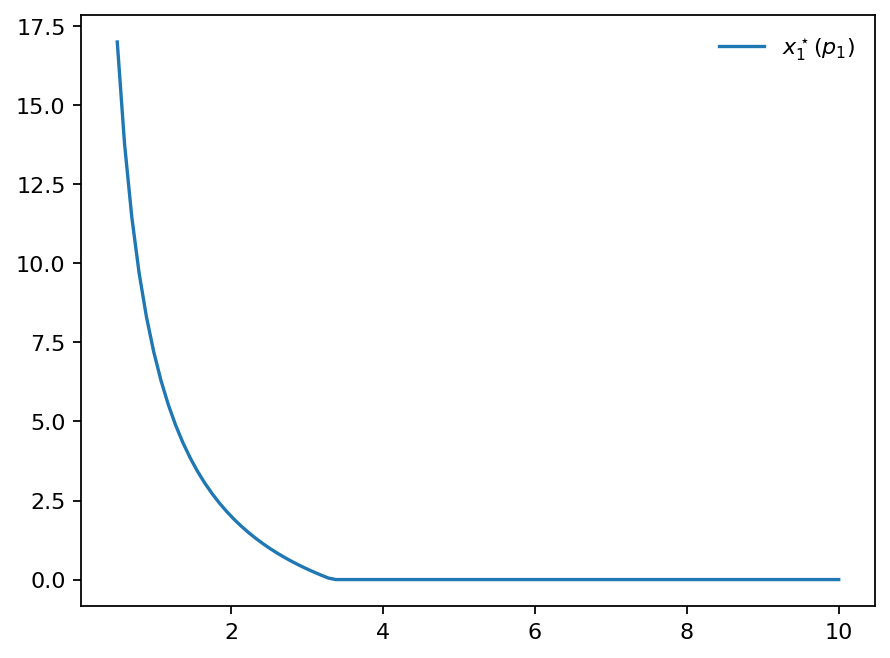
Fig. 111 Optimal choice of \(x_1\) as a function of \(p_1\) (aka demand curve)

Show code cell source Hide code cell source

alpha = 1
beta = 3
m = 10
cond = lambda p1: p1/m <= alpha/beta
f = lambda p: cond(p[0])*( beta * p[0] / (alpha *p[1]) ) + (1-cond(p[0])) * (m / p[1])
lb,ub = .5,5
x = y = np.linspace(lb,ub, 100)
X, Y = np.meshgrid(x, y)
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)
fig = plt.figure(dpi=160)
ax3 = fig.add_subplot(111, projection='3d')
ax3.plot_surface(X, Y, Z, 
            rstride=2, 
            cstride=2,
            alpha=0.7,
            linewidth=0.25)
plt.setp(ax3,xticks=[],yticks=[],zticks=[])
ax3.view_init(elev=22, azim=123)
plt.show()

Fig. 112 Optimal choice of \(x_2\) as a function of \((p_1,p_2)\) (aka demand curve)

References and reading

References

• [Simon and Blume, 1994]: 19.1, 19.2

• [Sundaram, 1996]: chapter 9, 5.2.3

Further reading and self-learning

• Mark Walker’s video lectures on correspondences