🛟 Midterm exam practice#
First and foremost, practice by going through the solutions of all of the tutorial problems. They are the best resource in preparation for the exam.
Week |
Topic |
||
|---|---|---|---|
\(\alpha\) |
alpha |
2 |
|
\(\beta\) |
beta |
3 |
|
\(\gamma\) |
gamma |
4 |
|
\(\delta\) |
delta |
5 |
|
\(\epsilon\) |
epsilon |
6 |
Additional problems are provided below.
Let \(f \colon \mathbb{R} \to \mathbb{R}\) be defined by \(f(x) = \sin(x)\).
Write down the set of stationary points of this function.
Which of these, if any, are maximizers, and which are minimizers?
The set \(S\) of stationary points of \(f\) are the points \(x \in \mathbb{R}\) such that \(f'(x) = \cos(x) = 0\). By the definition of the cosine function this is the set
Every point in the domain \(\mathbb{R}\) is interior (i.e, not an end point) and the function \(f\) is differentiable, so the set of maximizers will be contained in the set of stationary points. The same is true of the set of minimizers. From the definition of the sine function, we have
Hence the set of maximizers is
The set of minimizers is
Find all stationary points of the function \(f(x, y) = \frac{\cos(x^2 + y^2)}{1 + x^2 + y^2}\).
Find all maximizers and minimizers of this function on \(\mathbb{R}^2\).
It is always helpful to try to plot the function first. The graph of \(f(x,y)\) is
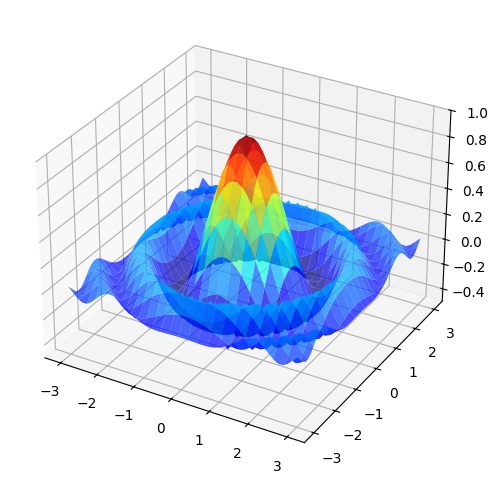
Let \(t = x^2+y^2 \geq 0\). The function becomes
First note that since \(t \geq 0\) and \(\cos(t) \leq 1\), we have \(g(t)\leq 1\) and \(g(0)=1\). Hence, \(t=0\) is a maximizer for \(g\), or \((x,y)=(0,0)\) is the maximizer for \(f\). It is a unique maximizer, since if \(g(t) < 1\) for \(t >0\).
Next, we find the stationary points of \(f\) by finding the stationary points of \(g\). The FOC is
Since \((1+t)^2>0\), it must be
The numerical solutions for the smallest stationary point \(t_m\) such that \(\cos(t_m)<0\) are
‘The smallest stationary point is tm=2.889969697678371’
‘The minimum is -0.24897613487740497’
The minimizers are \(\{(x,y)\in\mathbb{R}: x^2+y^2 = t_m\}\). To verify that \(t_m\) is the unique minimizer for \(g\), since \(\cos^2(t) + \sin^2(t)=1\), we rewrite FOC to get
Therefore, the smallest stationary point such that \(\cos(t) < 0\) will be the unique minimizer for \(g\).
For a function \(f \colon \mathbb{R}^2 \ni (x,y) \mapsto 2x^2+y^4-2xy \in \mathbb{R}\) write down the gradient and the Hessian, find the stationary points (those points where gradient is equal to zero vector), and compute the Hessian at those points.
COMING SOON
For a function \(f \colon \mathbb{R}^2 \ni (x,y) \mapsto 2xy-x^2-y^4 \in \mathbb{R}\) write down the gradient and the Hessian, find the stationary points (those points where gradient is equal to zero vector), and compute the Hessian at those points.
COMING SOON
