🔬 Tutorial problems kappa

Show code cell content Hide code cell content

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from myst_nb import glue


f = lambda x: x[0]**3/3 - 3*x[1]**2 + 2*x[0]
gx = lambda y: y**3/4
gy = lambda x: (4*x)**(1/3)

x = y = np.linspace(-5.0, 5.0, 100)
X, Y = np.meshgrid(x, y)
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)

ymax = gy(5.0)
y = np.linspace(-ymax, ymax, 100)
X1,Y1 = gx(y),y
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X1), np.ravel(Y1))])
Z1 = zs.reshape(X1.shape)

fig = plt.figure(dpi=160)
ax1 = fig.add_subplot(111)
ax1.set_aspect('equal', 'box')
ax1.contour(X, Y, Z, 50,
            cmap=cm.jet)
ax1.plot(X1, Y1)
plt.setp(ax1, xticks=[],yticks=[])
glue("pic1", fig, display=False)

fig = plt.figure(dpi=160)
ax2 = fig.add_subplot(111, projection='3d')
ax2.plot_wireframe(X, Y, Z,
            rstride=2,
            cstride=2,
            alpha=0.7,
            linewidth=0.25)
f0 = f(np.zeros((2)))+0.1
ax2.plot(X1, Y1, Z1, c='red')
plt.setp(ax2,xticks=[],yticks=[],zticks=[])
ax2.view_init(elev=18, azim=-160)
glue("pic2", fig, display=False)

\(\kappa\).1

Formulation

Solve the following constrained maximization problem using the Lagrange method, including the second order conditions.

\[\begin{split} f(x,y) = \frac{x^3}{3}-3y^2+2x \to \max_{x,y} \\ \text {subject to} \\ 4x = y^3,\\ x,y \in \mathbb{R} \end{split}\]

Hint

Follow standard algorithm of Lagrange method.

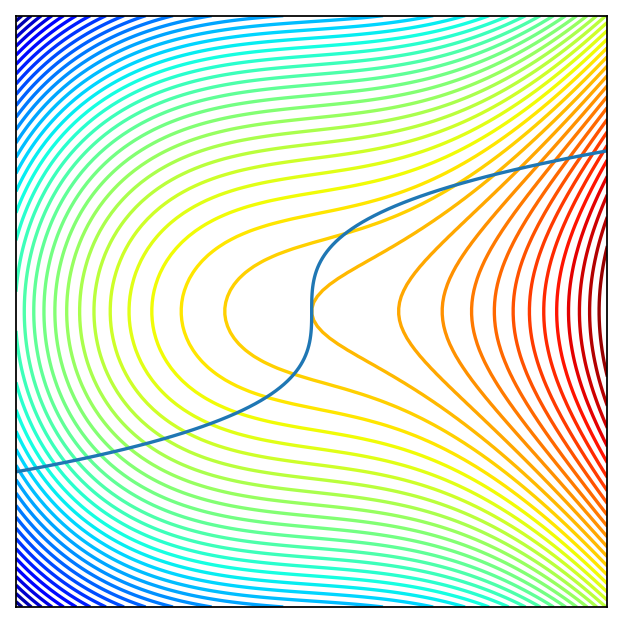
Fig. 95 Level curves of the criterion function and constraint curve.

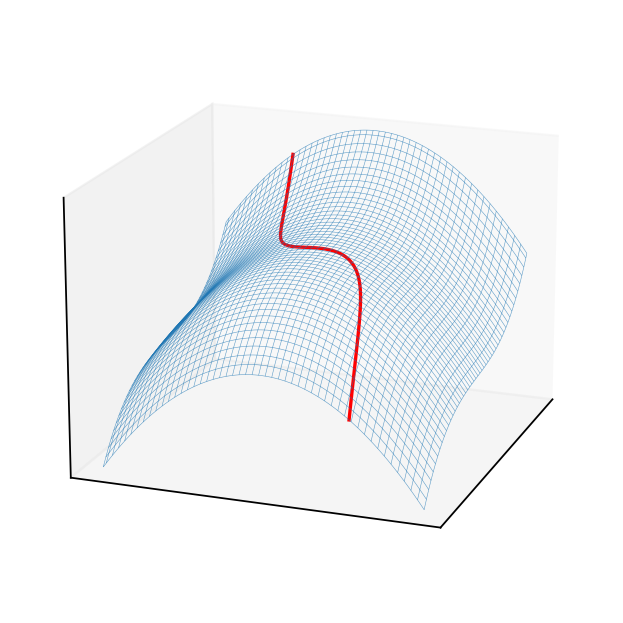
Fig. 96 3D plot of the criterion surface with the constraint curve projected to it.

Solution

Let \(f(x,y)= x^3/3 - 3y^2 + 2x\) and \(g(x,y)=4x-y^3\) for all \(x,y \in \mathbb{R}\). The constraint set is \(\{(x,y): g(x,y)=0\}\). The Lagrangian function is

\[ \mathcal{L}(x,y,\lambda) = f(x,y) - \lambda g(x,y) = f(x,y)= x^3/3 - 3y^2 + 2x - \lambda(4x-y^3) \]

The first order partial derivatives are

\[\begin{split} \frac{\partial \mathcal{L}}{\partial x}= x^2 + 2 - 4 \lambda, \quad \\ \frac{\partial \mathcal{L}}{\partial y}= -6y + 3\lambda y^2, \quad \\ \frac{\partial \mathcal{L}}{\partial \lambda}= -(4x -y^3). \end{split}\]

The bordered Hessian matrix is

\[\begin{split} H \mathcal{L}(x,y,\lambda)) = \begin{pmatrix} 0 & \frac{\partial^2 \mathcal{L}}{\partial \lambda \partial x} & \frac{\partial^2 \mathcal{L}}{\partial \lambda \partial y}\\ \frac{\partial^2 \mathcal{L}}{\partial \lambda \partial x}& \frac{\partial^2 \mathcal{L}}{\partial x^2} & \frac{\partial^2 \mathcal{L}}{\partial x \partial y} \\ \frac{\partial^2 \mathcal{L}}{\partial \lambda \partial y}& \frac{\partial^2 \mathcal{L}}{\partial y \partial x} & \frac{\partial^2 \mathcal{L}}{\partial y^2} \end{pmatrix} = \begin{pmatrix} 0& -4& 3y^2 \\ -4& 2x & 0\\ 3y^2& 0&-6 + 6 \lambda y \end{pmatrix}. \end{split}\]

Observe that \(\mathrm{rank}(Dg)) = \mathrm{rank}((-4, 3 y^2)) = 1\) for all \(x,y \in \mathbb{R}\). That is, the constrained qualification holds for all points on the constraint.

The first order conditions are

\[\begin{split} \frac{\partial \mathcal{L}}{\partial x}= x^2 + 2 - 4 \lambda =0, \quad \\ \frac{\partial \mathcal{L}}{\partial y}= -6y + 3\lambda y^2 =0, \quad \\ \frac{\partial \mathcal{L}}{\partial \lambda}= -(4x -y^3)=0. \end{split}\]

Observe that if \(\lambda=0\), then the FOCs imply \(x^2+2-4\lambda = x^2+2 = 0\), which is a contradiction since \(x^2+2 \ge 2\). It must be that \(\lambda \ne 0\). Next, from the equation \(-6y+3\lambda y^2 = 3y(\lambda y -2)=0\), it is either \(y=0\) or \(y = \lambda/2\).

Case 1: Suppose that \(y=0\). Then, from the constraint \(4x=y^3\) we get \(x=0\). Also, the FOC yields \(x^2+2 - 4\lambda = 0+2-4\lambda=0\) so that \(\lambda=1/2\). Hence, the optimizer is \((x^*, y^*, \lambda^*)=(0,0,1/2)\). The corresponding bordered Hessian matrix is

\[\begin{split} H\mathcal{L}(0,0,1/2)= \begin{pmatrix} 0 &-4 & 0\\ -4& 0&0\\ 0 &0& -6 \end{pmatrix} \end{split}\]

Since there are two variables \(N=2\) and one constraint \(K=1\), it suffices to check the last (\(N-K=1\)) leading principal minor, i.e., the determinant of the full bordered Hessian matrix. The determinant follows

\[\begin{split} \det (H\mathcal{L})=0 - (-4)\begin{vmatrix}-4&0 \\ 0& -6 \end{vmatrix} = 96 >0. \end{split}\]

It has the same sign as \((-1)^N=(-1)^2\). Therefore, the bordered Hessian matrix is negative definite and \((x^*, y^*, \lambda^*)=(0,0,1/2)\) is a local maximizer on the constraint set.

Case 2: Suppose that \(y=2/\lambda\). Then, by \(\lambda = 2/y\) and \(x = y^3/4\), the FOCs yield

\[\begin{split} x^2 + 2 - 4 \lambda = y^6/16 + 2 - 8/y = 0 \\ \Rightarrow y^7 + 32 y - 128=0 \end{split}\]

Let \(h(y)=y^7 + 32 y - 128\). Since \(h'(y)=7 y^6+32 >0\), function \(h\) is strictly increasing. Note that the solution for \(h(y)=0\) is strictly positive since \(y^7\) and \(y\) have the same sign. We can verify that \(y^* \approx 1.8325\) solves \(h(y)=0\). The optimizer is \((x^*, y^*,\lambda^*)=(\bar{y}^{3}/4, \bar{y}, 2/\bar{y})\) where \(\bar{y}\) satisfies \(h(\bar{y})=0\). The corresponding bordered Hessian is

\[\begin{split} H\mathcal{L}(\bar{y}^{3}/4, \bar{y}, 2/\bar{y})= \begin{pmatrix} 0& -4& 3 \bar{y}^{2} \\ -4& 2(\bar{y}^{3}/4) & 0\\ 3y^2& 0&-6 + 6 (2/\bar{y}) \bar{y} \end{pmatrix} = \begin{pmatrix} 0& -4& 3 \bar{y}^{2} \\ -4& \bar{y}^{3}/2 & 0\\ 3y^2& 0&6 \end{pmatrix}. \end{split}\]

The determinant is

\[\begin{split} \det (H\mathcal{L})= - (-4)\begin{vmatrix}-4& 3\bar{y}^2 \\ 0& 6 \end{vmatrix} +3 \bar{y}^2 \begin{vmatrix}-4& 3\bar{y}^2 \\ \bar{y}^3/2& 0 \end{vmatrix} = -\frac{9}{2}\bar{y}^7 - 96 <0, \end{split}\]

where the last inequality holds since \(\bar{y}\) is positive. Therefore, \(H\mathcal{L}\) has the same sign as \((-1)^K= -1\) so that it is positive definite. Hence, \((x^*, y^*,\lambda^*)=(\bar{y}^{3}/4, \bar{y}, 2/\bar{y})\) is a local minimizer on the constraint set.

Finally, since \(f(x,y) = x^3/3-3y^2+2x = x^3-3(4x)^{1/3}+2x \rightarrow \infty\) as \(x \rightarrow \infty\), there is no global maximizer. The local maximizer on the constraint is \((x,y)=(0,0)\).

\(\kappa\).2

Formulation

Find the maxima and minima of the function

\[ f(x,y) = xy \text{ subject to } x^2+y^2=2a^2, a>0 \]

Check both first and second order conditions.

Hint

Follow standard algorithm of Lagrange method.

Solution

We first wite down the Lagrangian:

\[ \mathcal{L}(x, y, \lambda) = xy - \lambda(x^2 + y^2 - 2a^2). \]

We have:

\[ \nabla \mathcal{L}(\lambda, x, y) = \left( \begin{array}{ccc} -(x^2 + y^2 - 2a^2), & y - 2\lambda x, & x - 2\lambda y \end{array} \right). \]

F.O.C.s are \(\nabla \mathcal{L}(\lambda, x, y) = 0\).

If \(\lambda = 0\), then \(x=y=0\), which contradicts with \(x^2 + y^2 - 2a^2 = 0\) because \(a>0\). Thus, \(\lambda \neq 0\).

If \(x=0\), then \(\lambda = y = 0\), which contradicts with \(\lambda \neq 0\). Thus, \(x \neq 0\).

Similarly, we can prove \(y \neq 0\).

Thus, we have \(y = 2 \lambda x\), \(x = 2 \lambda y\) and \(x,y,\lambda \ne 0\). Combining the two equation we have \(y = 4 \lambda^2 y\) and \(\lambda^2 = 1/4\). Consider the two cases one by one: for \(\lambda = 1/2\) we have \(x=y\), and for \(\lambda = -1/2\) we have \(x=-y\). Taking into account the constraint, each of the two cases leads to two each, namely \(x=\pm a\) and \(y= \pm a\).

Altogether we get four critical points:

1. \(x=a, y=a, \lambda = \frac{1}{2}\),

2. \(x=a, y=-a, \lambda = -\frac{1}{2}\),

3. \(x=-a, y=a, \lambda = -\frac{1}{2}\),

4. \(x=-a, y=-a, \lambda = \frac{1}{2}\).

The bordered Hessian:

\[\begin{split} H\mathcal{L}(\lambda, x, y) = \left[ \begin{array}{ccc} 0 & -2x & -2y \\ -2x & -2\lambda & 1 \\ -2y & 1 & -2\lambda \\ \end{array} \right] \end{split}\]

Since there are two variables, one constraint (\(N=2\), \(K=1\), \(N-K=1\)), we only need to check the sign of the determinant of the bordered Hessian (the last leading principal minor):

\[ \det(H\mathcal{L}(\lambda, x, y)) = 8\big(xy + \lambda (x^2 + y^2)\big). \]

Notice that:

\[\begin{split} \begin{array}{rl} & \det(H\mathcal{L}(1/2, a, a)) = \det(H\mathcal{L}(1/2, -a, -a)) = 16a^2 > 0, \\ & \det(H\mathcal{L}(-1/2, -a, a)) = \det(H\mathcal{L}(-1/2, a, -a)) = -16a^2 < 0. \end{array} \end{split}\]

Since \((-1)^K=-1\), we conclude that the critical points \((a, a)\) and \((-a, -a)\) satisfy the pattern for negative definiteness, and the critical points \((-a, a)\) and \((a, -a)\) satisfy the pattern for positive definiteness. Thus, the critical points \((a, a)\) and \((-a, -a)\) are local maximizers, and the critical points \((a, -a)\) and \((-a, a)\) are local minimizers.

In this question, the gloabl maximizer/minimizer exists by Weierstrass theorem and must be some local maximizer/minimizer. From \(f(a, a) = f(-a, -a) = a^2, f(-a, a) = f(a, -a) = -a^2\), we know the maxima is \(a^2\) and the minima is \(-a^2\).

\(\kappa\).3

Formulation

Find the maxima and minima of the function

\[ f(x,y) = \tfrac{1}{x} + \tfrac{1}{y} \]

subject to

\[ (\tfrac{1}{x})^2+(\tfrac{1}{y})^2=(\tfrac{1}{a})^2, \]

where \(a>0\).

Hint

Follow standard algorithm of Lagrange method.

Solution

We first wite down the Lagrangian:

\[ \mathcal{L}(x, y, \lambda) = \frac{1}{x} + \frac{1}{y} - \lambda (\frac{1}{x^2} + \frac{1}{y^2} - \frac{1}{a^2}). \]

The F.O.C.s are:

\[\begin{split} \nabla \mathcal{L}(\lambda, x, y) = [\begin{array}{ccc} -(\frac{1}{x^2} + \frac{1}{y^2} - \frac{1}{a^2}), & -\frac{1}{x^2} + \frac{2\lambda}{x^3}, & -\frac{1}{y^2} + \frac{2\lambda}{y^3} \\ \end{array}] = 0. \end{split}\]

Solving F.O.C.s, we get two solutions:

1. \(x=y=\sqrt{2}a, \lambda = \frac{\sqrt{2}}{2}a.\)

2. \(x=y=-\sqrt{2}a, \lambda = -\frac{\sqrt{2}}{2}a.\)

The bordered Hessian:

\[\begin{split} H\mathcal{L}(\lambda, x, y) = \left[ \begin{array}{ccc} 0 & 2/x^3 & 2/y^3 \\ 2/x^3 & 2/x^3 - 6\lambda/x^4 & 0 \\ 2/y^3 & 0 & 2/y^3 - 6\lambda/y^4 \\ \end{array} \right] \end{split}\]

Since there are two variables, one constraint (\(N=2\), \(K=1\), \(N-K=1\)), we only need to check the sign of the determinant of the bordered Hessian (the last leading principal minor):

\[ \det(H\mathcal{L}(\lambda, x, y)) = -8 \Big( \frac{y-3\lambda}{x^6y^4} + \frac{x-3\lambda}{x^4y^6} \Big). \]

Since for both critical points, we have \(x=y=2\lambda\), we only need to consider \(\det(H\mathcal{L}(x/2, x, x)) = 8/x^9\).

Notice that:

\[\begin{split} \begin{array}{rl} &\det(H\mathcal{L}(\frac{\sqrt{2}}{2}a, \sqrt{2}a, \sqrt{2}a)) = \frac{8}{{(\sqrt{2}a)}^9} > 0. \\ &\det(H\mathcal{L}(-\frac{\sqrt{2}}{2}a, -\sqrt{2}a, -\sqrt{2}a)) = \frac{8}{{(-\sqrt{2}a)}^9} < 0. \end{array} \end{split}\]

Thus, we know that the critical point \((\sqrt{2}a, \sqrt{2}a)\) is local maximizer, and the critical points \((-\sqrt{2}a, -\sqrt{2}a)\) are local minimizers.

In this question, the gloabl maximizer/minimizer exists by Weierstrass theorem and must be some local maximizer/minimizer. We know the maxima is \(f(\sqrt{2}a, \sqrt{2}a) = \frac{\sqrt{2}}{a}\) and the minima is \(f(-\sqrt{2}a, -\sqrt{2}a) = -\frac{\sqrt{2}}{a}\).

\(\kappa\).4

Formulation

Solve the following maximization problem

\[\begin{split} xy^{\tfrac{1}{2}}z^{\tfrac{1}{3}} \longrightarrow max_{x,y,z} \\ \text{ subject to }\quad\quad\\ x \ge 0, y \ge 0 ,z \ge 0,\\ 3x + 2y + z \le 10\\ \end{split}\]

Hint

Follow standard algorithm of Lagrange method.

Solution

First, notice that if \(x=0\), \(f(0, y,z) = 0 < f(1, 1, 1)=1\), thus, \(x>0\). Similarly, we can prove \(y > 0\) and \(z > 0\).

Second, notice that if \(x + 2y + z < 10\), we can set \(x^{\prime} = 10 - 2y - z\), which implies \(x^{\prime} > x\) and \(f(x^{\prime}, y, z) > f(x, y, z)\).

Thus, the only binding constraint is \(x + 2y + z = 10\).

The Lagrangian is:

\[ \mathcal{L}(x, y, z, \lambda) = x y^{1/2}z^{1/3} - \lambda (3x + 2y + z -10). \]

The gradient of the Lagrangian w.r.t. \((\lambda, x, y, z)\) is:

\[\begin{split} \nabla \mathcal{L}(\lambda, x, y, z) = \begin{pmatrix} -(3x + 2y + z -10)\\ y^{1/2}z^{1/3} - 3\lambda\\ \frac{1}{2}x y^{-1/2}z^{1/3} - 2\lambda\\ \frac{1}{3}x y^{1/2}z^{-2/3} - \lambda \\ \end{pmatrix}. \end{split}\]

Solve \(\nabla \mathcal{L}(\lambda, x, y, z) = 0\), we get \(x = z = \frac{20}{11}\), \(y = \frac{15}{11}\).

The bordered Hessian:

\[\begin{split} H\mathcal{L}(\lambda, x, y, z) = \begin{bmatrix} 0 & -3 & -2 & -1 \\ -3 & 0 & \frac{1}{2}y^{-1/2}z^{1/3} & \frac{1}{3}y^{1/2}z^{-2/3} \\ -2 & \frac{1}{2}y^{-1/2}z^{1/3} & -\frac{1}{4}xy^{-3/2}z^{1/3} & \frac{1}{6}xy^{-1/2}z^{-2/3} \\ -1 & \frac{1}{3}y^{1/2}z^{-2/3} & \frac{1}{6}xy^{-1/2}z^{-2/3} & -\frac{2}{9}xy^{1/2}z^{-5/3} \\ \end{bmatrix}. \end{split}\]

Since there are three variables, one constraint (\(N=3\), \(K=1\), \(N-K=2\)), we need to check two last leading principal minors of \(H\mathcal{L}\), that is the determinant of the bordered Hessian and the determinant of the \(H\mathcal{L}\) where last column and last row are removed. Denote the matrix composed of the intersection of first three rows and first three columns of \(H\mathcal{L}\) by \(M(\lambda, x, y, z)\).

We can simplify \(H\mathcal{L}\) by using \(x = z = \frac{4}{3}y\) at the critical point:

\[\begin{split} H\mathcal{L}(\lambda, z, \frac{3}{4}z, z) = \begin{bmatrix} 0 & -3 & -2 & -1 \\ -3 & 0 & \frac{\sqrt{3}}{3}z^{-1/6} & \frac{\sqrt{3}}{6}z^{-1/6} \\ -2 & \frac{\sqrt{3}}{3}z^{-1/6} & -\frac{2\sqrt{3}}{9}z^{-1/6} & \frac{\sqrt{3}}{9}z^{-1/6} \\ -1 & \frac{\sqrt{3}}{6}z^{-1/6} & \frac{\sqrt{3}}{9}z^{-1/6} & -\frac{\sqrt{3}}{9}z^{-1/6}\\ \end{bmatrix}. \end{split}\]

The determinants are:

\[ \det(H\mathcal{L}(\lambda, z, \frac{3}{4}z, z)) = -\frac{11}{3}z^{-1/3} < 0 \]

and

\[ \det(M(\lambda, z, \frac{3}{4}z, z)) = 6\sqrt{3}z^{-1/6} > 0 \]

since \(z = 20/11\) at the critical point.

Thus, the sign of the last leading principal minor is negative, and the sign of the determinant of the last but one leading principal minor is positive (recall there are three variables, and we need to confirm \(H_{(x, y, z)}\mathcal{L}(\lambda, x, y, z)\) is negative definite on the constraint set). Thus, the critical point is a local maximizer.

By Weierstrass theorem, we know the unique local maximizer must be the global maximizer. The maxima is \(f(20/11, 15/11, 20/11) = (\frac{20}{11})^{4/3} (\frac{15}{11})^{1/2}\).